Raum linearer stetiger Operatoren
Für zwei lineare (stetige) Operatoren 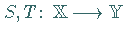 sind die Summe
sind die Summe 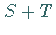 und das Vielfache
und das Vielfache 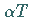 punktweise erklärt:
punktweise erklärt:
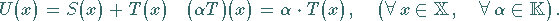 |
(12.134) |
Die Menge 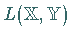 ,
häufig auch mit
,
häufig auch mit 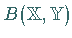 bezeichnet, aller linearen stetigen
Operatoren
bezeichnet, aller linearen stetigen
Operatoren  aus
aus  in
in 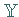 wird so ein Vektorraum, auf dem sich
wird so ein Vektorraum, auf dem sich 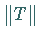 (12.129) als Norm erweist.
Dadurch wird
(12.129) als Norm erweist.
Dadurch wird 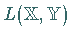 ein normierter Raum und, falls
ein normierter Raum und, falls 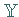 ein BANACH-Raum ist,
sogar ein BANACH-Raum.
Insbesondere sind also die Axiome
ein BANACH-Raum ist,
sogar ein BANACH-Raum.
Insbesondere sind also die Axiome 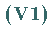 bis
bis 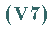 und
und
 bis
bis  erfüllt.
erfüllt.
Ist  ,
dann kann man für zwei beliebige Elemente
,
dann kann man für zwei beliebige Elemente 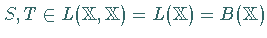 durch
durch
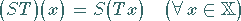 |
(12.135) |
das Produkt definieren, das den Axiomen 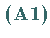 bis
bis 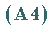 aus
normierte Algebren sowie der Verträglichkeitsbedingung
(12.98) mit der Norm genügt und so
aus
normierte Algebren sowie der Verträglichkeitsbedingung
(12.98) mit der Norm genügt und so 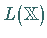 zu einer
(im allgemeinen nichtkommutativen) normierten und, falls
zu einer
(im allgemeinen nichtkommutativen) normierten und, falls  BANACH-Raum ist, zu
einer BANACH-Algebra macht.
Damit sind für jeden Operator
BANACH-Raum ist, zu
einer BANACH-Algebra macht.
Damit sind für jeden Operator 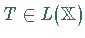 die Potenzen
die Potenzen
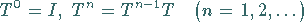 |
(12.136) |
definiert, wobei 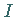 der identische Operator
der identische Operator 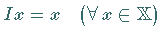 ist.
Es gilt
ist.
Es gilt
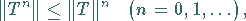 |
(12.137) |
und außerdem existiert stets der (endliche) Grenzwert
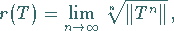 |
(12.138) |
der Spektralradius des Operators  heißt und den Beziehungen
heißt und den Beziehungen
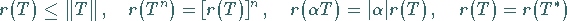 |
(12.139) |
genügt, wobei 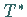 der zu
der zu  adjungierte Operator ist
(s. auch (12.173)).
adjungierte Operator ist
(s. auch (12.173)).
Im Falle der Vollständigkeit von 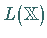 hat der Operator
hat der Operator 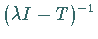 für
für
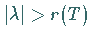 die Darstellung in Form der
NEUMANNschen Reihe
die Darstellung in Form der
NEUMANNschen Reihe
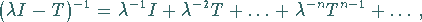 |
(12.140) |
die für 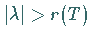 in der Operatornorm von
in der Operatornorm von 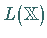 konvergiert.
konvergiert.
(S. auch Konvergenz der NEUMANNschen Reihe).
![]() ,
dann kann man für zwei beliebige Elemente
,
dann kann man für zwei beliebige Elemente ![]() durch
durch