Konvergenz von Operatorenfolgen
1. Punktweise Konvergenz einer Folge von linearen stetigen Operatoren
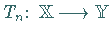zu einem Operator
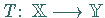liegt vor, wenn in 
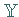gilt:
 |
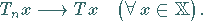(12.141) |
2. Gleichmäßige Konvergenz Die übliche Norm-Konvergenz einer
Operatorenfolge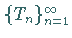 
im Raum 
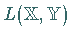zu 
,
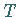also
 |
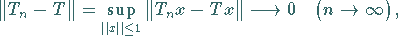(12.142) |
ist die gleichmäßige Konvergenz auf der Einheitskugel von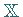 
.
Sie impliziert die punktweise Konvergenz, während die Umkehrung im allgemeinen nicht
gilt.
Anwendungen: Konvergenz von Quadraturformeln, wenn die Anzahl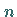 
der Stützstellen
gegen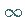 
geht, Permanenzprinzip von Summations- und Limitierungsverfahren u.a.
