|
|
|
|
ein Maßraum und 
eine reelle Zahl 
.
Für eine meßbare Funktion 
ist 
ebenfalls meßbar, so daß
)
ist.
Eine meßbare Funktion 
heißt
zur -ten Potenz integrierbar , -fach integrierbar oder
-fach summierbar , wenn 
gilt oder, äquivalent dazu,
wenn
integrierbar ist.
Für jedes
mit 
bezeichnet man mit 
oder
oder ganz ausführlich mit 
die Menge
aller zur -ten Potenz bezüglich 
auf 
summierbaren Funktionen, wobei für
die vereinfachte Bezeichnung 
vereinbart wird und für 
die
Funktionen quadratisch summierbar heißen.
Mit 
bezeichnet man die Menge aller meßbaren
-f.ü. beschränkten Funktionen auf
und definiert das wesentliche
Supremum einer Funktion
als
für alle 
ein Vektorraum und
eine Halbnorm auf 
.
Mit der Vereinbarung, 
zu schreiben, wenn
-f.ü. gilt, wird 
sogar ein Vektorverband.
Zwei Funktionen 
nennt man äquivalent (oder deklariert
man als gleich), wenn 
-f.ü. auf .
Auf diese Weise werden Funktionen, die -f.ü. übereinstimmen,
identifiziert.
Somit gewinnt man (mittels Faktorisierung der Menge
nach dem linearen
Teilraum 
)
eine Menge von Äquivalenzklassen, auf die kanonisch die
algebraischen Operationen und die Ordnung übertragen werden können, so daß sich
wieder ein Vektorverband ergibt, der jetzt mit 
oder 
(und
entsprechend ausführlicher) bezeichnet wird.
Seine Elemente heißen nach wie vor Funktionen, obwohl sie in Wirklichkeit Klassen
äquivalenter Funktionen sind.
Von Bedeutung ist nun, daß 
auf
eine Norm ist
(
steht dabei für die aus der Funktion
hervorgegange Äquivalenzklasse,
die im weiteren einfach wieder mit
bezeichnet wird), und 
für
alle
mit 
ein BANACH-Verband mit vielen guten
Verträglichkeitsbedingungen zwischen Norm und Ordnung, bei
mit
als Skalarprodukt sogar ein HILBERT-Raum wird
(s. Lit. 12.15).
Häufig wird für eine meßbare Teilmenge 
der Raum 
betrachtet.
Seine Definition bereitet wegen Schritt 5 bei der Einführung des
Integrals aber keine Schwierigkeiten.
Die Räume 
ergeben sich auch als
Vervollständigung (s. auch Abschnitt
BANACH-Räume) des mit der Integralnorm
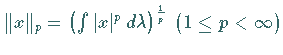versehenen nichtvollständigen normierten Raumes 
aller stetigen
Funktionen auf der Menge
(s. Lit. 12.21).
Sei
eine Menge von endlichem Maß, d.h. 
,
und gelte für
die Beziehung 
.
Dann gelten 
und mit einer nicht von 
abhängenden Konstanten 
für 
die
Abschätzung 
,
wobei 
die Norm des Raums
bezeichnet.
|
|
