1. Voraussetzungen:
Seien 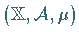 ein
ein 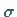 -endlicher Maßraum, d.h., es existiert eine
Folge
-endlicher Maßraum, d.h., es existiert eine
Folge
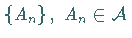 ,
so daß
,
so daß  und
und 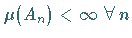 gilt.
In diesem Falle heißt das Maß
gilt.
In diesem Falle heißt das Maß 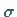 - endlich .
Es heißt endlich , wenn
- endlich .
Es heißt endlich , wenn 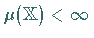 ,
und
Wahrscheinlichkeitsmaß , wenn
,
und
Wahrscheinlichkeitsmaß , wenn 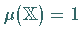 gilt.
Eine auf
gilt.
Eine auf 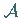 gegebene reelle Funktion
gegebene reelle Funktion 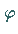 heißt absolutstetig
bezüglich
heißt absolutstetig
bezüglich 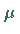 ,
wenn
,
wenn 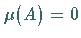 die Gleichung
die Gleichung 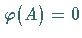 impliziert.
Die Bezeichnung dafür ist
impliziert.
Die Bezeichnung dafür ist 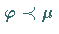 .
.
Für eine integrierbare Funktion  ist die auf
ist die auf 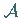 definierte Funktion
definierte Funktion
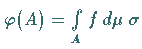 -additiv und absolutstetig bezüglich des
Maßes
-additiv und absolutstetig bezüglich des
Maßes 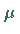 .
Fundamental für viele theoretische Untersuchungen und praktische Anwendungen ist die
Umkehrung dieses Fakts:
.
Fundamental für viele theoretische Untersuchungen und praktische Anwendungen ist die
Umkehrung dieses Fakts:
2. Satz von Radon-Nikodym:Seien eine 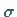 -additive Funktion
-additive Funktion 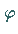 und ein Maß
und ein Maß 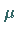 auf einer
auf einer
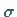 -Algebra
-Algebra 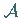 gegeben und sei
gegeben und sei 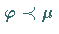 .
Dann existiert eine
.
Dann existiert eine 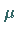 -integrierbare Funktion
-integrierbare Funktion  so, daß für jede Menge
so, daß für jede Menge
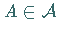 die Beziehung
die Beziehung
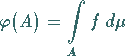 |
(12.206) |
gilt.
Die Funktion  ist dabei bis auf ihre Äquivalenzklasse eindeutig bestimmt, und
ist dabei bis auf ihre Äquivalenzklasse eindeutig bestimmt, und
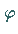 ist nichtnegativ genau dann, wenn
ist nichtnegativ genau dann, wenn 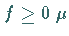 -f.ü.
-f.ü.
![]() ist die auf
ist die auf ![]() definierte Funktion
definierte Funktion
![]() -additiv und absolutstetig bezüglich des
Maßes
-additiv und absolutstetig bezüglich des
Maßes ![]() .
Fundamental für viele theoretische Untersuchungen und praktische Anwendungen ist die
Umkehrung dieses Fakts:
.
Fundamental für viele theoretische Untersuchungen und praktische Anwendungen ist die
Umkehrung dieses Fakts:
![]() -additive Funktion
-additive Funktion ![]() und ein Maß
und ein Maß ![]() auf einer
auf einer
![]() -Algebra
-Algebra ![]() gegeben und sei
gegeben und sei ![]() .
Dann existiert eine
.
Dann existiert eine ![]() -integrierbare Funktion
-integrierbare Funktion ![]() so, daß für jede Menge
so, daß für jede Menge
![]() die Beziehung
die Beziehung