Konvergenzsätze
1. Satz von B. Levi über die monotone Konvergenz:
Sei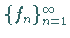 
eine fast überall monoton wachsende Folge nichtnegativer
integrierbarer Funktionen mit Werten in 
.
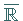Dann gilt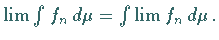 
2. Satz von Fatou:
Sei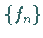 
eine Folge nichtnegativer 
-wertiger meßbarer
Funktionen. Dann gilt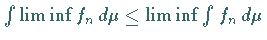 
.
3. Satz von Lebesgue über dominante oder majorisierte Konvergenz:
Sei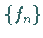
eine Folge von meßbaren Funktionen, die auf 
fast überall
konvergiert.
Wenn es eine solche integrierbare Funktion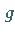 
mit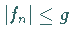 
fast überall gibt,
dann ist 
integrierbar und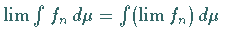 
.
