Vervollständigung eines metrischen Raumes
Jeder beliebige, also im allgemeinen nicht vollständige metrische Raum 
kann
vervollständigt werden; genauer, es existiert ein metrischer Raum 
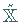mit
folgenden Eigenschaften:
1.
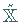enthält einen zu
isometrischen Teilraum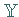 
.
2.
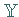ist überall dicht in 
.
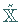3.
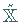ist ein vollständiger metrischer Raum.
4. Ist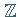 
ein beliebiger metrischer Raum mit den Eigenschaften 1. bis
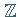3., dann sind
und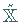
isometrisch.
Der dadurch bis auf Isometrie eindeutig bestimmte vollständige metrische Raum heißt
die Vervollständigung des Raumes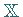 
.
