Sei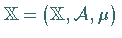 
.
Das Integral 
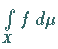(oder auch mit 
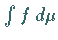bezeichnet) für
meßbare Funktionen 
wird schrittweise wie folgt definiert:
1.
sei eine Elementarfunktion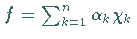 
,
dann setzt
man
 |
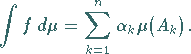(12.199) |
2. Ist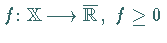 
,
dann
setzt man
 |
(12.200) |
3. Ist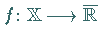 
und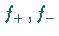 
positiver bzw. negativer Teil von 
,
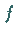dann setzt man
 |
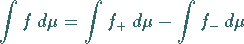(12.201) |
unter der Bedingung, daß wenigstens eines der Integrale auf der rechten Seite endlich
ist, um den unbestimmten Ausdruck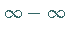 
zu vermeiden.
4. Für eine komplexwertige Funktion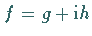 
setzt man, falls für
die Funktionen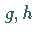 
die nach (12.201) definierten Integrale endlich sind,
 |
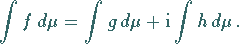(12.202) |
5. Kann für eine meßbare Menge 
und eine Funktion
nach den angegebenen
Festlegungen das Integral der Funktion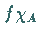 
definiert werden, dann setzt man
 |
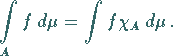(12.203) |
Das Integral einer meßbaren Funktion ist im allgemeinen eine Zahl aus
.
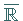Eine Funktion
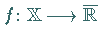nennt man
integrierbar oder summierbar über 
bezüglich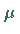 
,
wenn sie meßbar ist und 
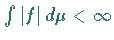gilt.
