Integration der homogenen partiellen linearen Differentialgleichung
Die Integration der homogenen partiellen linearen Differentialgleichung ist der
Integration des sogenannten charakteristischen Systems
 |
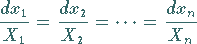(9.69a) |
äquivalent.
Zur Lösung dieses Systems können zwei Wege eingeschlagen werden:
1. Man kann als unabhängige Variable ein beliebiges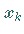 
auswählen, für das
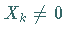gilt, so daß das System in die Form
 |
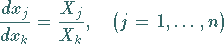(9.69b) |
übergeht.
2. Bequemer ist es, unter Beibehaltung der Symmetrie eine neue unabhängige
Variable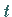 
einzuführen, indem
 |
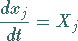(9.69c) |
gesetzt wird.
Jedes erste Integral des Systems (9.69a) ist eine Lösung der
homogenen linearen partiellen Differentialgleichung (9.68b)
und umgekehrt, jede Lösung von (9.68b) ist ein erstes Integral
von (9.68a) (s. Allgemeine Lösung).
Wenn hierbei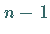 
erste Integrale
 |
(9.69d) |
unabhängig sind (s. Fundamentalsystem von Lösungen), dann gilt
 |
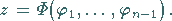(9.69e) |
Dabei ist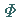 
eine beliebige Funktion der
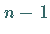Argumente 
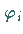und eine
allgemeine Lösung der homogenen linearen Differentialgleichung von
(9.68a).
