Allgemeine Lösung
Konstanten:
Die allgemeine Lösung der Differentialgleichung (9.4) enthält 
unabhängige willkürliche Konstanten:
 |
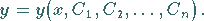(9.26a) |
Geometrische Bedeutung:
Geometrisch betrachtet, wird durch die Gleichung (9.26a)
eine -parametrige Schar von Integralkurven definiert.
Jede einzelne dieser Integralkurven, d.h. das Kurvenbild der entsprechenden
partikulären Lösung, kann durch spezielle Wahl der willkürlichen Konstanten
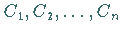erhalten werden.
Wenn das partikuläre Integral den oben angegebenen Anfangsbedingungen genügen soll,
dann müssen die Werte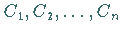
aus den folgenden Gleichungen ermittelt
werden:
Sollten diese Gleichungen für die willkürlichen Anfangswerte in einem bestimmten
Gebiet einander widersprechen, dann ist die Lösung in diesem Gebiet nicht allgemein,
d.h., die Konstanten sind nicht unabhängig voneinander wählbar.
Berechnung eines ersten Integrals:
Auch die allgemeine Lösung des Systems (9.23a) enthält
willkürliche Konstanten.
Diese allgemeine Lösung läßt sich auf zweierlei Weise darstellen, entweder
aufgelöst nach den unbekannten Funktionen
 |
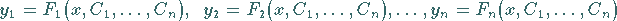(9.27a) |
oder aufgelöst nach den willkürlichen Konstanten
 |
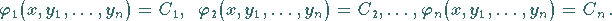(9.27b) |
Im Falle von (9.26b) ist jede Beziehung der Art
 |
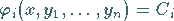(9.27c) |
ein erstes Integral des Systems (9.23a).
Das erste Integral kann unabhängig vom allgemeinen Integral als Beziehung der Art
(9.27c) definiert werden.
Dabei wird davon ausgegangen, daß (9.27c) zur Identität
wird, wenn anstelle der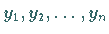 
irgendeine partikuläre Lösung des
gegebenen Systems mit einer durch diese partikuläre Lösung bestimmten willkürlichen
Konstanten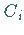 
eingesetzt wird.
Wenn irgendein erstes Integral der Form (9.27c) bekannt ist, dann
genügt die Funktion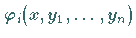 
der partiellen
Differentialgleichung
 |
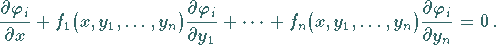(9.27d) |
Umgekehrt, jede Lösung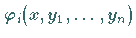
der Differentialgleichung
(9.27d) liefert ein erstes Integral des Systems
(9.23a) in der Form
(9.27c).
Das allgemeine Integral des Systems (9.27a) kann aus einem System
von
ersten Integralen des Systems (9.23a) gebildet werden,
für die die zugehörigen Funktionen
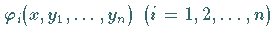linear unabhängig sind.
