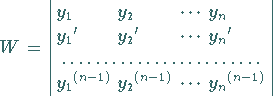Fundamentalsystem von Lösungen
Ein System von  Lösungen
Lösungen 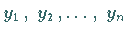 einer homogenen linearen
Differentialgleichung wird Fundamentalsystem genannt, falls diese Funktionen in
dem betrachteten Intervall linear unabhängig sind, also ihre Linearkombination
einer homogenen linearen
Differentialgleichung wird Fundamentalsystem genannt, falls diese Funktionen in
dem betrachteten Intervall linear unabhängig sind, also ihre Linearkombination
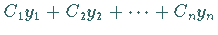 für kein Wertesystem der
für kein Wertesystem der 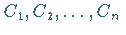 ,
ausgenommen für
,
ausgenommen für 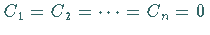 ,
identisch verschwindet, d.h. für alle
,
identisch verschwindet, d.h. für alle
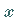 -Werte in dem betreffenden Intervall.
-Werte in dem betreffenden Intervall.
Die Lösungen 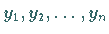 einer linearen homogenen Differentialgleichung
bilden genau dann ein Fundamentalsystem, wenn ihre WRONSKI-Determinante
einer linearen homogenen Differentialgleichung
bilden genau dann ein Fundamentalsystem, wenn ihre WRONSKI-Determinante
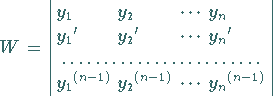 |
(9.34) |
von Null verschieden ist.
Für jedes Lösungssystem einer homogenen linearen Differentialgleichung gilt die
Formel von LIOUVILLE :
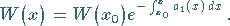 |
(9.35) |
Aus dieser Gleichung folgt, daß die WRONSKI-Determinante nur identisch
verschwinden kann.
Das bedeutet:
Die  Lösungen
Lösungen 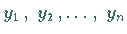 der homogenen linearen
Differentialgleichung sind genau dann linear abhängig, wenn nur an einer einzigen Stelle
der homogenen linearen
Differentialgleichung sind genau dann linear abhängig, wenn nur an einer einzigen Stelle
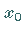 des betrachteten Intervalls
des betrachteten Intervalls 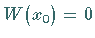 gilt.
Wenn dagegen die Lösungen
gilt.
Wenn dagegen die Lösungen 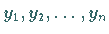 ein Fundamentalsystem von Lösungen
bilden, dann lautet die allgemeine Lösung der linearen homogenen Differentialgleichung
(9.33)
ein Fundamentalsystem von Lösungen
bilden, dann lautet die allgemeine Lösung der linearen homogenen Differentialgleichung
(9.33)
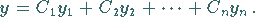 |
(9.36) |