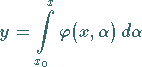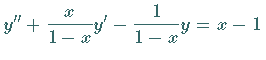Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        
Themen dieser Seite


Lösung der inhomogenen Differentialgleichung mittels Quadraturen

Wenn das Fundamentalsystem von Lösungen der zur inhomogenen Differentialgleichung gehörenden homogenen Differentialgleichung bekannt ist, stehen die folgenden zwei Lösungsverfahren zur Verfügung:


Methode der Variation der Konstanten

Die gesuchte Lösung wird in der Form
(9.38a)

aufgeschrieben. Die werden nicht als Konstanten aufgefaßt, sondern als Funktionen von . Danach wird die Erfüllung der Gleichungen
 
(9.38b)
     
 

gefordert. Einsetzen von in (9.33) ergibt
(9.38c)

Darauf folgt die Lösung des linearen Gleichungssystems (9.38b) und (9.38c) zur Bestimmung der
deren Integrale die liefern.

Beispiel

.
In den Intervallen 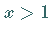bzw. 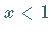sind alle Voraussetzungen über die Koeffizienten erfüllt. Zuerst wird die homogene Gleichung 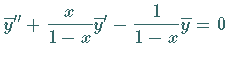gelöst. Eine partikuläre Lösung ist 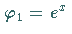. Der Ansatz 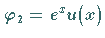ergibt für 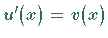die Differentialgleichung 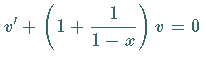. Eine Lösung dieser Differentialgleichung ist 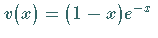, und somit ist 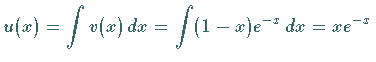. Damit ergibt sich die zweite Lösung 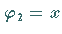. Die allgemeine Lösung der homogenen Gleichung ist daher 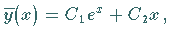. Variation der Konstanten ergibt jetzt:




also

Damit ist die allgemeine Lösung der inhomogenen Differentialgleichung:

Methode von Cauchy

In der allgemeinen Lösung
(9.39a)

der zu (9.33) gehörenden homogenen Differentialgleichung werden die Konstanten derart bestimmt, daß für den beliebigen Parameter die Gleichungen für erfüllt sind. Auf diese Weise erhält man eine spezielle Lösung der homogenen Differentialgleichung, die mit bezeichnet werden soll, und
(9.39b)

ist dann eine partikuläre Lösung der inhomogenen Differentialgleichung (9.33), die an der Stelle gemeinsam mit ihren Ableitungen bis zur Ordnung einschließlich verschwindet.

Beispiel

Für die mit der Methode der Variation der Konstantengelöste Differentialgleichung (9.39a), für die für die allgemeine Lösung der homogenen Differentialgleichung ist, folgt aus , so daß die partikuläre Lösung der inhomogenen Differentialgleichung mit lautet: . Hieraus kann man auch die allgemeine Lösung der inhomogenen Differentialgleichung gewinnen.