Auftreten
Die parametrisch getriebene, gedämpfte NLS-Gleichung (engl. PDNLS) tritt auf
- bei der FARADAY-Resonanz in der Dynamik der Fluide
(Flüssigkeiten und Gase),
- bei der paramagnetischen erzeugung von Spinwellen in Ferromagnatika und
Antiferromagnatika,
- in der nichtlinearen Optik,
- in FRENKEL-KONTOROVA-Systemen.
Gleichung und Lösungen
Die (von I.V. BARASHENKOV et. al. seit 1991 behandelte) PDNLS-Gleichung
 |
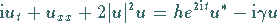(9.164) |
hat zwei Parameter (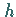
Antriebsstärke, 
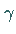Reibungskoeffizient), von deren
Werten die Stabiliät der Lösungen sehr empfindlich abhängt.
Die folgende Abbildung zeigt ein Stabilitätsdiagramm der Lösungen der
PDNLS-Gleichung.
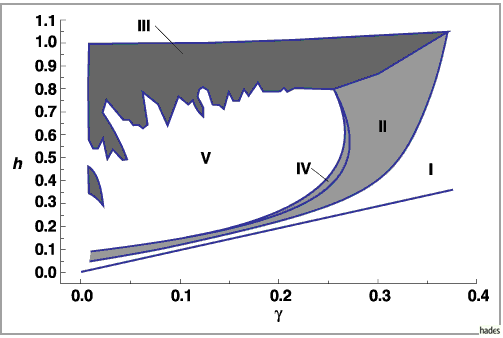
Gebiet I (s. Abbildung):
In Gebiet I oberhalb der Linie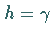 
ist das Soliton
 |
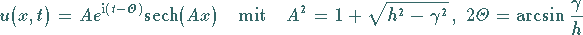(9.165) |
eine stationäre Lösung.
Dieses PDLNS-Soliton wird parametrisches Pumpen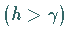 
stabilisiert.
Gebiet II (s. Abbildung):
Im Gebiet II ist das PDLNS-Soliton instabil: Amplitude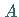 
und
Phase 
ändern sich periodisch.
Diese Instabilität führt zu zwei Szenarien des Überganges zum Chaos:
- Ein Szenarium führt über Quasiperiodizität zum raum-zeitlichen Chaos
(Gebiet III),
- ein zweites, das FEIGENBAUM-Szenarium,
führt zu Gebiet IV,
- Gebiet V (s. Abbildung) Hier gehen alle Lösungen
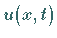für
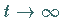asymptotisch in den Wert 
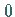über.
- In der
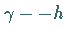-Ebene gibt es bei 
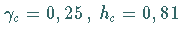einen trikritischen Punkt, an dem die zwei Szenarien und das Gebiet mit
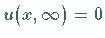zusammentreffen.
- Die Grenze zwischen den Gebieten III und V für
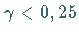nahe
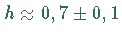erinnert an die ARNOLD-Zungen.
