Nichtlineare Evolutionsgleichungen
Unter einer Evolutionsgleichung versteht man eine Gleichung, die die zeitliche
Entwicklung einer physikalischen Größe beschreibt.
Beispiele für lineare Evolutionsgleichungen sind die Wellengleichung,
die Wärmeleitungsgleichung und die
SCHRÖDINGER-Gleichung.
Die Lösungen der Evolutionsgleichungen werden auch Evolutionsfunktionen
genannt.
Im Unterschied zu den linearen Evolutionsgleichungen enthalten die nichtlinearen
Evolutionsgleichungen (9.129), (9.130)
(9.131), (9.132) und (9.133) die
nichtlinearen Terme
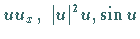 bzw.
bzw. 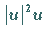 und
und 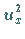 .
Diese Gleichungen sind, ausgenommen (9.132), parameterfrei.
Physikalisch betrachtet beschreiben nichtlineare Evolutionsgleichungen Strukturbildungen
wie Solitonen (dispersive Strukturen und periodische Muster) sowie nichtlineare Wellen
(dissipative Strukturen).
.
Diese Gleichungen sind, ausgenommen (9.132), parameterfrei.
Physikalisch betrachtet beschreiben nichtlineare Evolutionsgleichungen Strukturbildungen
wie Solitonen (dispersive Strukturen und periodische Muster) sowie nichtlineare Wellen
(dissipative Strukturen).