Solitonen -- man spricht auch von solitären Wellen -- sind physikalisch
betrachtet impuls- oder auch stufenförmig lokalisierte Störungen eines nichtlinearen
Mediums oder Feldes; die betreffende Energie ist auf ein enges Gebiet konzentriert.
Sie treten auf:
- in Festkörpern, z.B. in anharmonischen Gittern, in JOSEPHSON-Kontakten,
in Glasfasern (optische Solitonen), bei der Wanderung von BLOCH-Wänden und
in quasi-eindimensionalen Leitern ( PEIERLS-Phasenübergnge),
- in Flüssigkeiten als Oberflächenwellen (hohe Flutwellen in Flußmündungen,
Tsunamis, d.h. seismische Wasserwellen) oder Spinwellen,
- bei Wüstendünen als Barchane,
- in Plasmen als LANGMUIR-Solitonen,
- in linearen Molekülen (Proteinketten, z.B.
 -Helix als
DAWYDOW-Soliton),
-Helix als
DAWYDOW-Soliton),
- in der klassischen und Quantenfeldtheorie.
Solitonen haben sowohl Teilchen- als auch Welleneigenschaften; sie sind zu jedem Zeitpunkt
örtlich lokalisiert, und der Bereich der Lokalisierung, bzw. der Punkt, um den herum die
Welle lokalisiert ist, bewegt sich wie ein freies Teilchen; insbesondere kann er auch
ruhen.
Ein Soliton besitzt eine permanente Ausbreitungsstruktur:
Auf Grund einer Balance zwischen Nichtlinearität und Dispersion ändern sich Form und
Geschwindigkeit nicht.
Amplitude und Geschwindigkeit sind gekoppelt; ihrer Form nach unterscheidet man
glockenförmige und stufenförmige Solitonen.
Mathematisch betrachtet, sind Solitonen spezielle Lösungen bestimmter nichtlinearer
partieller Differentialgleichungen, die in Physik, Technik und angewandter Mathematik
auftreten.
Ihre Besonderheiten bestehen darin, daß sie konservativ sind (es fehlt jegliche
Dissipation) sowie vollständig integrabel.
Die nichtlinearen Terme können nicht störungstheoretisch behandelt werden.
Eine Lösungsmethode ist die Spektraltransformation.
Wichtige Beispiele für Gleichungen mit Solitonenlösungen sind:
a) Korteweg-de-Vries- (KdV)-Gleichung:
 |
(9.129) |
b) nichtlineare Schrödinger-(NLS)-Gleichung:
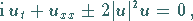 |
(9.130) |
c) Sinus-Gordon- (SG)-Gleichung:
 |
(9.131) |
Mit 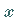 bzw.
bzw. 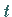 als Index werden partielle Ableitungen bezeichnet, z.B.
als Index werden partielle Ableitungen bezeichnet, z.B.
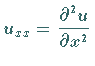 .
In diesen Gleichungen wird der eindimensionale Fall betrachtet, d.h., es gilt
.
In diesen Gleichungen wird der eindimensionale Fall betrachtet, d.h., es gilt
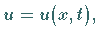 wobei
wobei 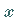 die Ortskoordinate und
die Ortskoordinate und 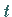 die Zeit repräsentieren.
Die Gleichungen sind in skalierter Form angegeben, d.h., die beiden unabhängigen
Variablen
die Zeit repräsentieren.
Die Gleichungen sind in skalierter Form angegeben, d.h., die beiden unabhängigen
Variablen 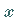 und
und 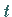 sind hier dimensionslose Größen.
Bei praktischen Anwendungen sind sie mit den für das jeweilige Problem
charakteristischen, dimensionsbehafteten Größen (Länge und Zeit) zu
multiplizieren.
Analoges gilt für die Geschwindigkeit
sind hier dimensionslose Größen.
Bei praktischen Anwendungen sind sie mit den für das jeweilige Problem
charakteristischen, dimensionsbehafteten Größen (Länge und Zeit) zu
multiplizieren.
Analoges gilt für die Geschwindigkeit 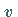 .
.
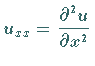 .
In diesen Gleichungen wird der eindimensionale Fall betrachtet, d.h., es gilt
.
In diesen Gleichungen wird der eindimensionale Fall betrachtet, d.h., es gilt