Themen dieser Seite
Begriff der Schrödinger-Gleichung
Bestimmung und Abhängigkeiten
Die SCHRÖDINGER-Gleichung, deren Lösungen, die Wellenfunktionen
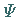 ,
die Eigenschaften eines quantenmechanischen Systems beschreiben, also die
Eigenschaften der Teilchenzustände zu berechnen gestatten, ist eine partielle
Differentialgleichung mit Ableitungen der Wellenfunktion 2. Ordnung für die
Raumkoordinaten und 1. Ordnung für die Zeitkoordinate:
,
die Eigenschaften eines quantenmechanischen Systems beschreiben, also die
Eigenschaften der Teilchenzustände zu berechnen gestatten, ist eine partielle
Differentialgleichung mit Ableitungen der Wellenfunktion 2. Ordnung für die
Raumkoordinaten und 1. Ordnung für die Zeitkoordinate:
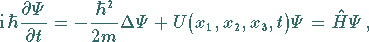 |
(9.109a) |
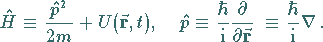 |
(9.109b) |
Hierbei sind 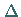 der LAPLACE-Operator,
der LAPLACE-Operator,
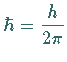 die reduzierte PLANCKsche Konstante,
i die
imaginäre Einheit und
die reduzierte PLANCKsche Konstante,
i die
imaginäre Einheit und  der Nablaoperator.
Zwischen dem Impuls
der Nablaoperator.
Zwischen dem Impuls 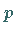 des betrachteten Teilchens mit der Masse
des betrachteten Teilchens mit der Masse 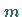 und seiner
Materiewellenlänge
und seiner
Materiewellenlänge 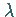 besteht die Beziehung
besteht die Beziehung 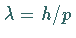 .
.
Besonderheiten
1. In der Quantenmechanik werden allen meßbaren Größen Operatoren
zugeordnet.
Der in (9.109a) und (9.109b) auftretende
HAMILTON-Operator 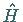 (,,Hamiltonian ``) stellt die
Gesamtenergie des Systems dar, die in kinetische und potentielle Energie aufgeteilt wird.
Der erste Term in
(,,Hamiltonian ``) stellt die
Gesamtenergie des Systems dar, die in kinetische und potentielle Energie aufgeteilt wird.
Der erste Term in 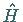 ist der Operator für die kinetische Energie, der zweite der
für die potentielle Energie.
ist der Operator für die kinetische Energie, der zweite der
für die potentielle Energie.
In der Quantenmechanik tritt an die Stelle der
HAMILTON-Funktion des klassischen mechanischen
Systems der HAMILTON-Operator.
2. Die imaginäre Einheit tritt in der SCHRÖDINGER-Gleichung explizit auf.
Daher sind die Wellenfunktionen komplexe Funktionen.
Für die Berechnung der beobachtbaren Größen sind die beiden reellen, in
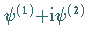 enthaltenen Funktionen erforderlich.
Das Quadrat
enthaltenen Funktionen erforderlich.
Das Quadrat 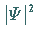 der Wellenfunktion, das die Aufenthaltswahrscheinlichkeit
der Wellenfunktion, das die Aufenthaltswahrscheinlichkeit
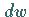 des Teilchens in jedem beliebigen Raumelement
des Teilchens in jedem beliebigen Raumelement 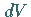 des betrachteten Gebietes
beschreibt, unterliegt speziellen zusätzlichen Bedingungen.
des betrachteten Gebietes
beschreibt, unterliegt speziellen zusätzlichen Bedingungen.
3. Jede spezielle Lösung hängt außer vom Potential der
Wechselwirkung ( Kraft ) von den Anfangs- und Randbedingungen des
gegebenen Problems ab.
Im allgemeinen handelt es sich um lineare Randwertprobleme 2. Ordnung, deren Lösungen
nur für die Eigenwerte physikalisch sinnvoll sind.
Sinnvolle Lösungen zeichnen sich dadurch aus, daß ihr Betragsquadrat überall
eindeutig und regulär ist und im Unendlichen verschwindet.
4. Auf Grund des Welle-Teilchen-Dualismus besitzen die Mikroteilchen
gleichzeitig Wellen- und Teilcheneigenschaften, so daß die
SCHRÖDINGER-Gleichung eine Wellengleichung für die
DE-BROGLIEschen Materie-Wellen ist.
5. Die Einschränkung auf nichtrelativistische Probleme bedeutet, daß die
Teilchengeschwindigkeit 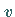 sehr viel kleiner sein muß als die Lichtgeschwindigkeit
sehr viel kleiner sein muß als die Lichtgeschwindigkeit
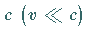 .
.
Ausführliche Darstellungen der Anwendungen der SCHRÖDINGER-Gleichung sind in
der Spezialliteratur der theoretischen Physik dargestellt
(s. z.B. Lit. 9.6, 9.8, 9.16,
22.17).
In diesem Kapitel werden lediglich einige wichtige Beispiele betrachtet.
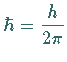 die reduzierte PLANCKsche Konstante,
i die
imaginäre Einheit und
die reduzierte PLANCKsche Konstante,
i die
imaginäre Einheit und