Den allgemeinen nichtrelativistischen Fall eines spinlosen Teilchens mit der Masse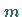 
und der Geschwindigkeit 
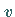im orts- und zeitabhängigen Potentialfeld 
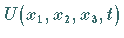beschreibt die zeitabhängige SCHRÖDINGER-Gleichung
(9.109a).
Die unter Besonderheiten aufgeführten speziellen Bedingungen, denen
die Wellenfunktion genügen muß, lauten:
a) Die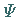 
-Funktion muß beschränkt und stetig sein.
b) Die partiellen Ableitungen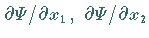 
und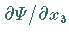 
müssen stetig sein.
c) Die Funktion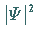 
muß integrierbar sein, also muß
 |
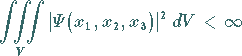(9.110a) |
gelten.
Gemäß Normierungsbedingung muß die Wahrscheinlichkeit, das Teilchen im
betrachteten Gebiet zu finden, gleich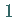 
sein.
Dazu reicht (9.110a) aus, weil das Integral stets durch einen Faktor vor
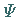auf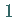
gebracht werden kann.
Eine Lösung der zeitabhängigen SCHRÖDINGER-Gleichung hat die Form
 |
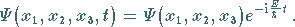(9.110b) |
Der Zustand des Teilchens wird in einem Zeitpunkt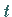 
durch eine periodische Funktion von
der Zeit mit der Kreisfrequenz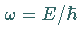 
beschrieben.
Wenn die Energie des Teilchens in dem Zustand den festen Wert 
besitzt, dann hängt die Wahrscheinlichkeit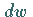 
,
es in einem Raumelement 
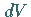zu
finden, nicht von der Zeit ab:
 |
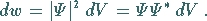(9.110c) |
Man spricht vom stationären Zustand des Teilchens.
