Konstruktion der Greenschen Funktion für das Dirichletsche Problem der
LAPLACEschen Differentialgleichung
 |
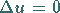(9.99a) |
für den Fall, daß das betrachtete Gebiet ein Kreis ist (s. Abbildung).
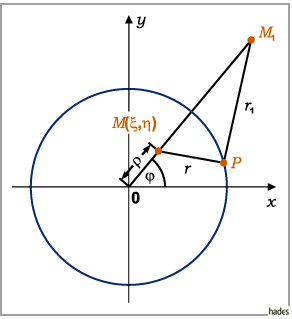
Die GREENsche Funktion lautet
 |
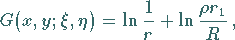(9.99b) |
wobei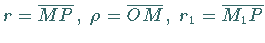 
und
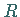der Radius des betrachteten Kreises ist.
Die Punkte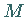 
und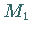 
liegen in bezug auf den Kreis symmetrisch, d.h., beide Punkte
liegen auf demselben Radiusstrahl, und es gilt
 |
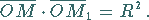(9.99c) |
Mit der angegebenen Formel (9.97e) zur Lösung des DIRICHLETschen
Problems ergibt sich nach Einsetzen der Normalenableitung der GREENschen Funktion
und einigen Umformungen das POISSONsche Integral
 |
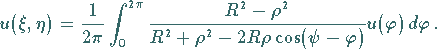(9.99d) |
Die Bezeichnungen sind die gleichen wie oben.
Mit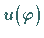 
werden die auf dem Kreisrand vorgegebenen Werte von 
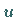beschrieben.
Für die Koordinaten des Punktes 
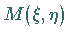gilt:
.
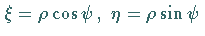