Laplacesche Differentialgleichung
Die Aufgabe der Bestimmung des Potentials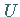 
eines Vektorfeldes 
,
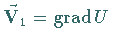in dem keine Quellen enthalten sind, führt gemäß (13.125) mit
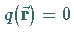auf
 |
(13.130a) |
d.h. auf die LAPLACEsche Differentialgleichung .
In kartesischen Koordinaten gilt:
 |
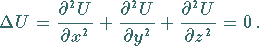(13.130b) |
Alle Funktionen, die dieser Differentialgleichung genügen, stetig sind und stetige
partielle Ableitungen erster und zweiter Ordnung besitzen, werden LAPLACEsche
oder harmonische Funktionen genannt.
Es werden drei grundlegende Fälle von Randwertaufgaben unterschieden:
1. Randwertaqufgabe (für das Innengebiet) oder
DIRICHLETsches Problem: Gesucht wird eine Funktion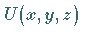 
,
die im Inneren eines gegebenen räumlichen bzw.
ebenen Gebietes harmonisch ist und auf dem Rand des Gebietes vorgegebene Werte annimmt.
2. Randwertaufgabe (für das Innengebiet) oder NEUMANNsches Problem :
Gesucht wird eine Funktion ,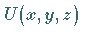
die im Inneren eines gegebenen Gebietes
harmonisch ist und deren Normalenableitung 
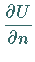auf dem Rand des
Gebietes vorgegebene Werte annimmt.
3. Randwertaufgabe (für das Innengebiet): Gesucht wird eine Funktion
,
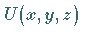die im Inneren eines Gebietes harmonisch ist, wobei auf dem Rand
des Gebietes der Ausdruck
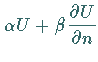
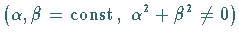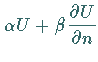
vorgegebene Werte annimmt.
