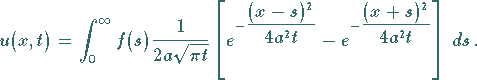Beispiel Wärmeleitungsgleichung
Die Wärmeausbreitung in einem homogenen Stab, dessen eines Ende im Unendlichen liegt,
während das andere unter konstanter Temperatur gehalten wird, beschreibt die lineare
partielle Differentialgleichung 2. Ordnung vom parabolischen Typ
 |
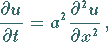(9.94a) |
die im Gebiet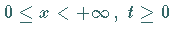 
den Anfangs- und Randbedingungen
 |
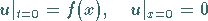(9.94b) |
genügt.
Dabei soll angenommen werden, daß die Temperatur im Unendlichen Null beträgt.
Zur Lösung wird die Methode der Variablentrennung
verwendet (s. auch
Wärmeleitungsgleichung für ein homogenes Medium).
Der Separationsansatz
 |
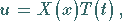(9.94c) |
eingesetzt in (9.94a), liefert die Beziehung
 |
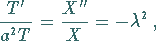(9.94d) |
wobei der Parameter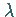 
in Analogie zu dem Vorgehen in den Beispielen A bis
D eingeführt wird.
Als Lösung für 
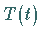erhält man
 |
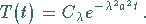(9.94e) |
Für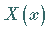 
ergibt sich mit der Randbedingung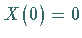 
 |
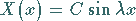(9.94f) |
und somit
 |
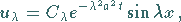(9.94g) |
wobei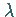
eine beliebige reelle Zahl sein kann.
Die Lösung kann daher in der Form
 |
(9.94h) |
angesetzt werden.
Aus der Anfangsbedingung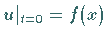 
folgt die Gleichung
 |
(9.94i) |
die erfüllt ist, wenn für die Konstante
 |
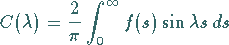(9.94j) |
wie bei der Bestimmung der FOURIER-Koeffizienten gesetzt wird.
Einsetzen in in (9.94i) ergibt
 |
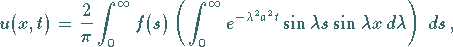(9.94k) |
und nach Ersetzen des Produkts der Sinus- durch eine
Differenz von Kosinusfunktionen (2.114) und
unter Benutzung von Formel (21.46) in der
Tabelle bestimmter Integrale erhält man schließlich
 |
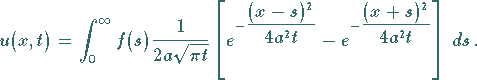(9.94l) |
