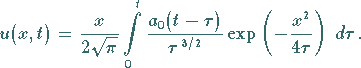Lösung der eindimensionalen Wärmeleitungsgleichung für ein homogenes Medium
1. Problemstellung
Die eindimensionale Wärmeleitungsgleichung mit verschwindendem Störglied und für
ein homogenes Medium sei in der Form
 |
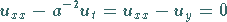(15.59a) |
in dem Grundgebiet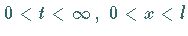 
und mit den Anfangs- und
Randbedingungen
 |
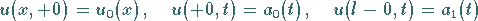(15.59b) |
gegeben.
Die Zeitkoordinate wurde durch die Substitution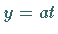 
ersetzt.
Wie die dreidimensionale Wärmeleitungsgleichung, so ist
auch (15.59a) vom parabolischen Typ.
2. Laplace-Transformation
Die Bildgleichung lautet
 |
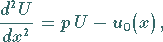(15.60a) |
die Randbedingungen sind
 |
(15.60b) |
Die Lösung der Bildgleichung lautet dann
 |
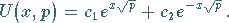(15.60c) |
Es ist von Vorteil, zunächst zwei Partikulärlösungen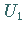 
und 
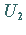mit der
Eigenschaft
 |
(15.61a) |
 |
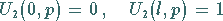(15.61b) |
herzustellen, d.h.
 |
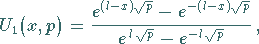(15.61c) |
 |
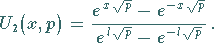(15.61d) |
Die gesuchte Lösung der Bildgleichung hat dann die Form
 |
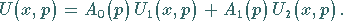(15.62) |
3. Rücktransformation
Die Rücktransformation ist im Falle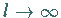 
besonders einfach und liefert:
 |
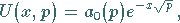(15.63a) |
 |
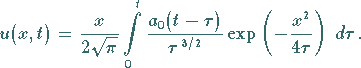(15.63b) |
