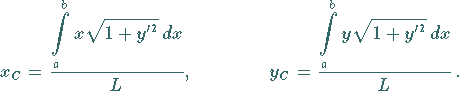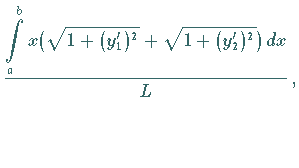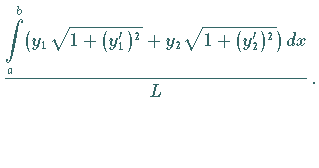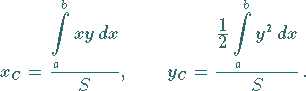Themen dieser Seite
Schwerpunkte, Guldinsche Regeln
1. Schwerpunkt des Bogenstückes
Der Schwerpunkt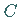 
des Bogenstückes einer homogenen ebenen Kurve 
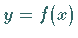im
Intervall 
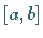mit der Länge 
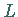(s. Abbildung) unter Berücksichtigung von
(8.60a):
 |
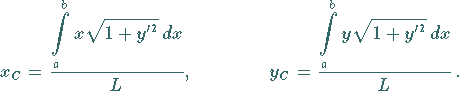(8.70) |
2. Schwerpunkt einer geschlossenen Kurve
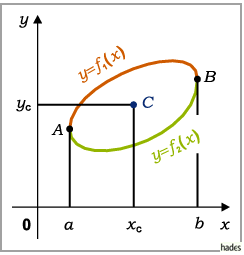
Der Schwerpunkt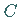
einer geschlossenen Kurve (s. Abbildung) mit den Gleichungen
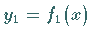für den oberen und 
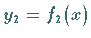für den unteren Kurventeil und
der Gesamtlänge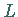
ergibt sich zu:
3. Erste Guldinsche Regel
Die Oberfläche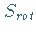 
eines Körpers, die bei Rotation eines ebenen
Kurvenstückes um eine Achse entsteht, die in der Ebene dieser Kurve liegt und die Kurve
nicht schneidet, ist gleich dem Produkt aus dem Umfang des Kreises, den der Schwerpunkt
des Kurvenstückes bei der Rotation im Abstand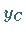 
von der Umdrehungsachse beschreibt,
also 
,
und der Länge des Kurvenstückes :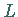
 |
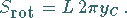(8.72) |
4. Schwerpunkt eines Trapezes
Der Schwerpunkt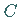
eines homogenen, zwischen den Kurvenpunkten 
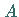und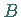 
krummlinig
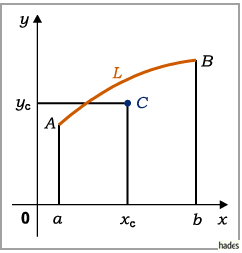
begrenzten Trapezes (s. Abbildung) mit dem Flächeninhalt 
des Trapezes und der
Gleichung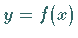
des Kurvenstückes 
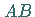ergibt sich zu:
 |
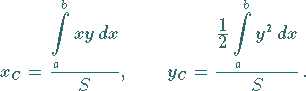(8.73) |
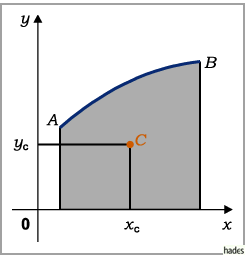
5. Schwerpunkt einer beliebigen ebenen Figur
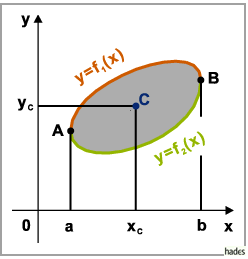
Der Schwerpunkt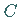
einer beliebigen ebenen Figur (s. Abbildung) mit der Fläche 
,
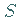oben und unten begrenzt durch Kurven mit den Gleichungen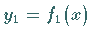
bzw.
,
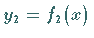berechnet sich gemäß:
 |
(8.74) |
Formeln zur Berechnung von Schwerpunkten mit Hilfe von Mehrfachintegralen sind in
der Tabelle Anwendung von Doppelintegralen und in der Tabelle
Anwendung von Dreifachintegralen angegeben.
6. Zweite Guldinsche Regel
Der Rauminhalt eines Körpers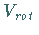 
,
der bei Rotation einer ebenen Figur um
eine Achse entsteht, die in der Figurenebene liegt und die Figur nicht schneidet,
ist gleich dem Produkt aus dem Umfang des Kreises, den der Schwerpunkt dieser
Fläche bei der Rotation beschreibt, also ,
und dem Flächeninhalt
der Figur :
 |
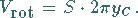(8.75) |
