(Siehe auch Zweite GULDINsche Regel.)
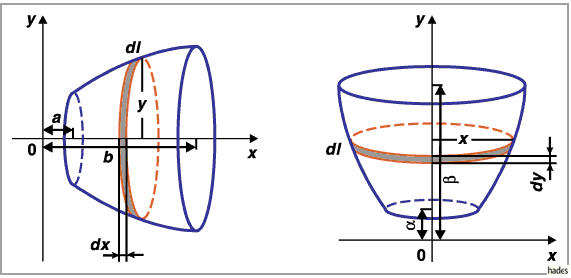
1. Volumen eines rotationssymmetrischen Körpers bei Drehung um
die 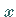 -Achse (s. linke Abbildung):
-Achse (s. linke Abbildung):
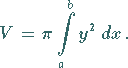 |
(8.62a) |
2. Volumen eines rotationssymmetrischen Körpers bei Drehung um
die 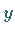 -Achse (s. rechte Abbildung):
-Achse (s. rechte Abbildung):
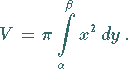 |
(8.62b) |
3. Volumen eines Körpers, wenn der Flächeninhalt seines senkrecht zur
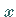 -Achse gelegten Querschnitts eine Funktion
-Achse gelegten Querschnitts eine Funktion 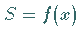 ist (s. Abbildung):
ist (s. Abbildung):
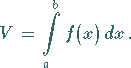 |
(8.63) |
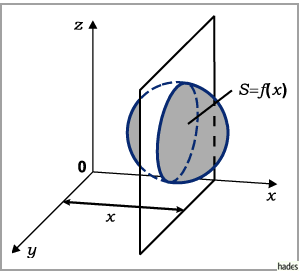
4. Cavalierisches Prinzip:
Existiert im Intervall 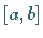 eine zweite Querschnittsfunktion
eine zweite Querschnittsfunktion
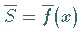 ,
die für jeden Abszissenwert
,
die für jeden Abszissenwert 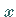 denselben
Wert hat wie
denselben
Wert hat wie 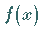 ,
so sind die Volumina
,
so sind die Volumina 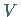 gemäß (8.63)
und
gemäß (8.63)
und 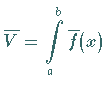 einander gleich.
einander gleich.
5.
Die Berechnung des Volumens komplizierterer Körper ist mit Hilfe des
Doppelintegrals oder mit Hilfe des Dreifachintegrals
möglich.
Formeln zur Berechnung von Volumina mit Hilfe von Mehrfachintegralen sind in
der Tabelle
Anwendung von Doppelintegralen und in der Tabelle
Anwendung von Dreifachintegralen angegeben.
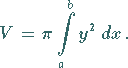
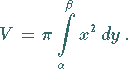
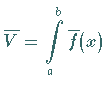 einander gleich.
einander gleich.