Definition des Doppelintegrals
Als Doppelintegral einer Funktion von zwei Veränderlichen 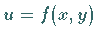 über einem
ebenen Flächenstück
über einem
ebenen Flächenstück  wird der Ausdruck
wird der Ausdruck
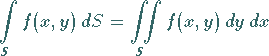 |
(8.134) |
bezeichnet.
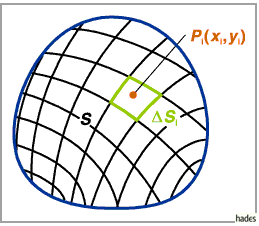
Es handelt sich dabei um einen Zahlenwert, der auf die folgende Weise ermittelt wird
(s. Abbildung):
1. Beliebige Zerlegung des Flächenstückes  in
in 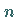 Elementarflächenstücke.
Elementarflächenstücke.
2. Auswahl eines beliebigen Punktes 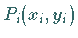 im Innern oder auf dem
Rande eines jeden Elementarflächenstückes.
im Innern oder auf dem
Rande eines jeden Elementarflächenstückes.
3. Multiplikation des Funktionswertes von 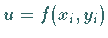 in diesem Punkt mit
dem Inhalt
in diesem Punkt mit
dem Inhalt 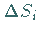 des entsprechenden Elementarflächenstückes.
des entsprechenden Elementarflächenstückes.
4. Addition aller so gewonnenen Produkte 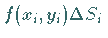 .
.
5. Berechnung des Grenzwertes der Summe
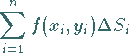 |
(8.135a) |
für den Fall, daß der Inhalt aller Elementarflächenstücke
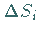 gegen Null geht, also ihre Anzahl
gegen Null geht, also ihre Anzahl 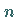 gegen
gegen  .
Dabei ist zu beachten, daß die Forderung,
.
Dabei ist zu beachten, daß die Forderung, 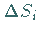 solle gegen Null streben,
allein nicht genügt.
Es muß sichergestellt sein, daß auch der Abstand der beiden am weitesten
voneinander entfernten Punkte, d.h. der Durchmesser des
Elementarflächenstückes , gegen Null geht, weil der Flächeninhalt eines Rechtecks
auch zu Null wird, wenn eine seiner Seiten Null gesetzt wird, der Durchmesser aber
endlich bleibt.
solle gegen Null streben,
allein nicht genügt.
Es muß sichergestellt sein, daß auch der Abstand der beiden am weitesten
voneinander entfernten Punkte, d.h. der Durchmesser des
Elementarflächenstückes , gegen Null geht, weil der Flächeninhalt eines Rechtecks
auch zu Null wird, wenn eine seiner Seiten Null gesetzt wird, der Durchmesser aber
endlich bleibt.
Wenn dieser Grenzwert existiert und von der Art der Einteilung des Flächenstückes
 in Elementarflächenstücke sowie von der Wahl der Punkte
in Elementarflächenstücke sowie von der Wahl der Punkte 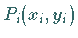 unabhängig
ist, dann wird er Doppelintegral der Funktion
unabhängig
ist, dann wird er Doppelintegral der Funktion 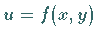 über dem Flächenstück
über dem Flächenstück
 ,
das Integrationsgebiet, genannt, und man schreibt:
,
das Integrationsgebiet, genannt, und man schreibt:
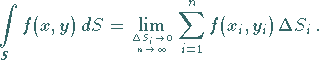 |
(8.135b) |
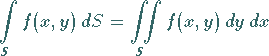
![]() in
in ![]() Elementarflächenstücke.
Elementarflächenstücke.
![]() im Innern oder auf dem
Rande eines jeden Elementarflächenstückes.
im Innern oder auf dem
Rande eines jeden Elementarflächenstückes.
![]() in diesem Punkt mit
dem Inhalt
in diesem Punkt mit
dem Inhalt ![]() des entsprechenden Elementarflächenstückes.
des entsprechenden Elementarflächenstückes.
![]() .
.
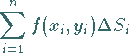
![]() gegen Null geht, also ihre Anzahl
gegen Null geht, also ihre Anzahl ![]() gegen
gegen ![]() .
Dabei ist zu beachten, daß die Forderung,
.
Dabei ist zu beachten, daß die Forderung, ![]() solle gegen Null streben,
allein nicht genügt.
Es muß sichergestellt sein, daß auch der Abstand der beiden am weitesten
voneinander entfernten Punkte, d.h. der Durchmesser des
Elementarflächenstückes , gegen Null geht, weil der Flächeninhalt eines Rechtecks
auch zu Null wird, wenn eine seiner Seiten Null gesetzt wird, der Durchmesser aber
endlich bleibt.
solle gegen Null streben,
allein nicht genügt.
Es muß sichergestellt sein, daß auch der Abstand der beiden am weitesten
voneinander entfernten Punkte, d.h. der Durchmesser des
Elementarflächenstückes , gegen Null geht, weil der Flächeninhalt eines Rechtecks
auch zu Null wird, wenn eine seiner Seiten Null gesetzt wird, der Durchmesser aber
endlich bleibt.