Normalteiler

Beispiel A
	bilden Untergruppen von bezüglich der Multiplikation.

Beispiel B
	Die geraden ganzen Zahlen bilden eine Untergruppe von bezüglich der Addition.

Beispiel C

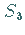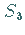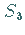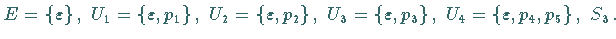
Untergruppen der Gruppe : Wegen des Satzes von LAGRANGE kann die 6-elementige Gruppe (außer den trivialen Untergruppen) nur Untergruppen mit 2 oder 3 Elementen haben. Tatsächlich hat die Gruppe folgende Untergruppen: Die nichttrivialen Untergruppen 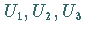und 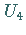sind zyklisch, weil ihre Elementeanzahlen sämtlich Primzahlen sind. Die 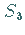ist dagegen nicht zyklisch. Außer den trivialen Normalteilern hat die Gruppe 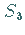nur noch die Untergruppe 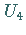als Normalteiler. 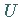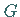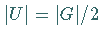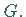Übrigens ist jede Untergruppe einer Gruppe mit Normalteiler von Alle symmetrischen Gruppen 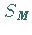und ihre Untergruppen werden Permutationsgruppen genannt.

Beispiel D
	Spezielle Untergruppen der Gruppe aller regulären Matrizen vom Typ bezüglich der Matrizenmultiplikation: Gruppe aller Matrizen mit der Determinante 1, Gruppe aller orthogonalen Matrizen, Gruppe aller orthogonalen Matrizen mit der Determinante 1. Die Gruppe ist Normalteiler von (s. Homomorphiesatz für Gruppen) und Normalteiler von

Beispiel E
	Als Untergruppen der Gruppe aller regulären komplexen Matrizen seien erwähnt: Gruppe aller unitären Matrizen, Gruppe aller unitären Matrizen mit der Determinante 1.