Drehung des Koordinatensystems
Wenn das kartesische Koordinatensystem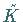 
aus 
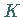durch Drehung hervorgeht, dann
gilt in (4.65) für die Transformationsmatrix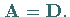 
Dabei ist 
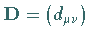die orthogonale Drehungsmatrix .
Die orthogonale Drehungsmatrix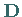 
hat die Eigenschaft
 |
(4.67a) |
Elemente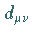 
von
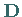sind die Richtungskosinusse der Winkel zwischen den
alten und neuen Koordinatenachsen.
Aus der Orthogonalität der Drehungsmatrix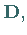 
d.h. aus
 |
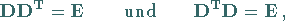(4.67b) |
folgt für ihre Elemente:
 |
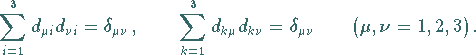(4.67c) |
Diese Gleichungen besagen, daß die Zeilen- und Spaltenvektoren der
Matrix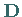
orthonormiert sind, denn 
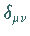ist das
KRONECKER-Symbol.
Die Elemente der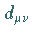
der Drehungsmatrix können auch mit Hilfe der
EULERschen Winkel dargestellt werden
(s. auch Drehung der Ebene und
Drehung im Raum).
