Koordinatentransformationen
Beim Übergang von einem kartesischen Koordinatensystem zu einem anderen ändern sich
die Koordinaten nach den folgenden Regeln:
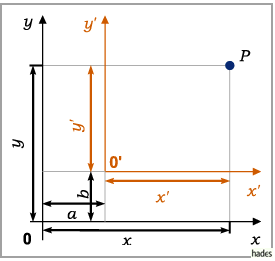
1. Parallelverschiebung der Koordinatenachsen um den Abszissen- bzw.
Ordinatenabschnitt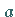 
bzw. 
,
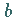so daß für die Koordinaten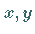 
vor der
Verschiebung,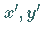 
nach der Verschiebung und für die Koordinaten 
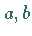des neuen
Koordinatenursprungs 0' im alten Koordinatensystem vor der Verschiebung gilt:
 |
(3.307a) |
 |
(3.307b) |
2. Drehung der Koordinatenachsen um den Winkel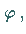 
so daß gilt:
 |
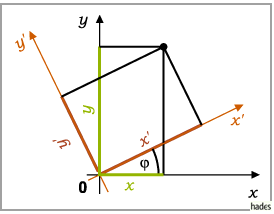
(3.308a) |
 |
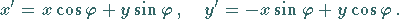(3.308b) |
Allgemein betrachtet läßt sich ein Übergang von einem Koordinatensystem in ein
anderes durch eine Transformation durchführen, die aus einer Translation und einer
Rotation, d.h. einer Drehung der Koordinatenachsen besteht.
Die zum diesem System aus zwei Gleichungen gehörende Koeffizientenmatrix lautet:
 |
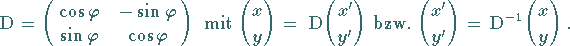(3.308c) |
Sie wird Drehungsmatrix genannt.
