|
Es ist die Kurve der Funktion 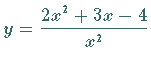 zu konstruieren:
zu konstruieren:
a) Die Funktion ist für alle 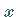 -Werte außer für -Werte außer für 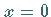 definiert.
definiert.
b) Es gibt keinerlei Symmetrie.
c) Für 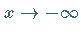 strebt
strebt 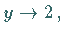 so daß
so daß 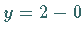 Annäherung von unten bedeutet, während sich für
Annäherung von unten bedeutet, während sich für 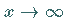 zwar ebenfalls
zwar ebenfalls
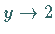 ergibt, aber
ergibt, aber 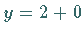 Annäherung von oben bedeutet.
Annäherung von oben bedeutet.
d) Bei 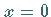 gibt es eine Unstetigkeitsstelle derart, daß die Kurve von
links und von rechts nach
gibt es eine Unstetigkeitsstelle derart, daß die Kurve von
links und von rechts nach 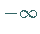 verläuft, da
verläuft, da 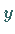 für kleine
für kleine 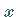 -Werte negativ
ist. -Werte negativ
ist.
e) Da 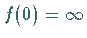 ist, gibt es keinen Schnittpunkt mit der
ist, gibt es keinen Schnittpunkt mit der 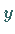 -Achse,
während -Achse,
während 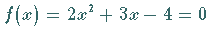 die Schnittpunkte mit der
die Schnittpunkte mit der 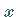 -Achse bei -Achse bei
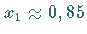 und
und 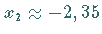 liefert.
liefert.
f) Ein Maximum liegt bei 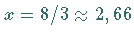 und
und 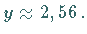
g) Ein Wendepunkt befindet sich bei 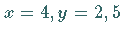 mit
mit
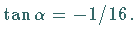
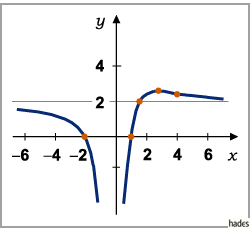
h) Nach der Skizzierung der Funktion auf Grund der gewonnenen Daten (s. Abbildung)
wird der Schnittpunkt der Kurve mit der Asymptote bei 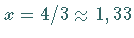 und
und
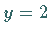 berechnet.
berechnet.
|