Definition der Funktion

Definition der Funktion

1. Funktion:Wenn

und

zwei variable Größen sind und wenn sich einem gegebenen

-Wert genau ein

-Wert zuordnen läßt, dann nennt man

eine Funktion von

und schreibt

(2.1)

Die veränderliche Größe

heißt unabhängige Variable oder Argument der Funktion

. Alle

-Werte, denen sich

-Werte zuordnen lassen, bilden den Definitionsbereich

der Funktion

. Die veränderliche Größe

heißt abhängige Variable ; alle

-Werte bilden den Wertebereich

der Funktion

. Funktionen können graphisch durch Punkte

als Kurven oder Funktionsgraphen dargestellt werden.
2. Reelle Funktion: Wenn Definitions- und Wertebereich nur reelle Zahlen enthalten, dann nennt man

eine reelle Funktion einer reellen Veränderlichen .

Beispiel A

mit

Beispiel B

mit

3. Funktion von mehreren Veränderlichen: Hängt die Variable von mehreren unabhängigen Variablen ab, dann bezeichnet man

(2.2)

als Funktion von mehreren Veränderlichen.
4. Komplexe Funktion: Wenn die unabhängige Variable eine komplexe Zahl

ist, dann wird durch

eine komplexe Funktion einer komplexen Veränderlichen beschrieben, zu deren Behandlung die Funktionentheorie benötigt wird. Zu den komplexen Funktionen gehören auch die komplexwertigen Funktionen , die für reelle Argumente

definiert sind, aber komplexe Funktionswerte besitzen.
5. Weitere Funktionen: In verschiedenen Anwendungsgebieten, z.B. in der Vektoranalysis und Feldtheorie, werden Funktionen verwendet, bei denen Argument- und Funktionswerte beispielsweise wie folgt definiert sind:

Argument reell - Funktion vektorwertig.

Beispiel A
	Vektorfunktion.

Beispiel B

Parameterdarstellung von Kurven.

Argument vektorwertig - Funktion reell.

Beispiel
	Skalarfeld.

Argument vektorwertig - Funktion vektorwertig.

Beispiel
	Vektorfeld.

6. Funktionale: Wird jeder Funktion

aus einer bestimmten Funktionenklasse eine reelle Zahl zugeordnet, dann spricht man von einem Funktional .

Beispiel A
	Ist eine gebene, über integrierbare Funktion, dann ist ein lineares Funktional bezüglich aller über stetigen Funktionen .

Beispiel B

Integralausdrücke bei Variationsaufgaben.

7. Funktion und Abbildung: Gegeben sind zwei nichtleere Menge und . Unter einer Abbildung , die durch

(2.3)

beschrieben wird, versteht man eine Vorschrift, die jedem Element

von

ein eindeutig bestimmtes Element

von

zuordnet. Das Element

heißt Bild von

, und man schreibt auch

. Die Menge

heißt Bildbereich oder Wertebereich von

, die Menge

heißt Originalbreich, Urbildbereich oder Definitionsbreich von

Beispiel A
	Sind Original- und Bildbereich Teilmengen der reellen Zahlen, d.h. gilt und , dann wird durch (2.3) eine reelle Funktion einer reellen Veränderlichen beschrieben.

Beispiel B

Ist 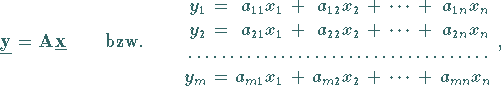eine Matrix vom Typ und gilt sowie , dann wird durch (2.3) eine Abbildung des in den beschrieben. Die Vorschrift (2.3) stellt dann das folgende System von linearen Gleichungen dar:

d.h. bedeutet das Produkt der Matrix mit dem Vektor .

Hinweise:

Durch den Begriff der Abbildung wird der Funktionsbegriff verallgemeinert. Deshalb werden Abbildungen auch als Funktionen bezeichnet.
Wichtige Eigenschaften von Abbildungen findet man im Abschnitt Abbildungen
Eine Abbildung, die jedem Element eines abstrakten Raumes eindeutig ein Element eines eventuellen anderen abstrakten Raumes zuordnet, wird Operator genannt. Dabei versteht man unter einem abstrakten Raum in der Regel einen Funktionenraum, da die Elemente der Räume, die für Anwendungen wichtig sind, meist Funktionen sind. Abstrakte Räume sind z.B. die linearen Räume (s. Vektorräume, metrische Räume und normierte Räume.

Beispiel B
	Ist eine Matrix vom Typ und gilt sowie , dann wird durch (2.3) eine Abbildung des in den beschrieben. Die Vorschrift (2.3) stellt dann das folgende System von linearen Gleichungen dar: d.h. bedeutet das Produkt der Matrix mit dem Vektor .