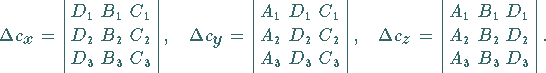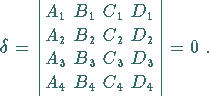Themen dieser Seite
Winkel zwischen zwei Ebenen, allgemeiner Fall
Die Winkel zwischen zwei Ebenen, gegeben durch die zwei Gleichungen
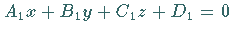 und
und 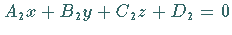 werden berechnet nach der Formel
werden berechnet nach der Formel
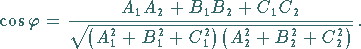 |
(3.405a) |
Sind die Ebenen durch die Vektorgleichungen 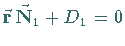 und
und
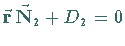 gegeben, dann gilt:
gegeben, dann gilt:
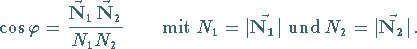 |
(3.405b) |
(Zum Skalarprodukt zweier Vektoren s. Skalarprodukt und
Skalarprodukt in affinen Koordinaten, zur Ebenengleichung
in Vektorschreibweise s. Vektorielle Gleichungen.)
Schnittpunkt dreier Ebenen
Die Koordinaten des Schnittpunktes dreier Ebenen, gegeben durch die drei Gleichungen
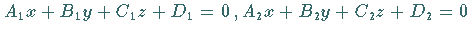 und
und 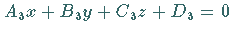 werden
berechnet nach den Formeln
werden
berechnet nach den Formeln
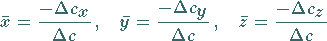 |
(3.406a) |
mit
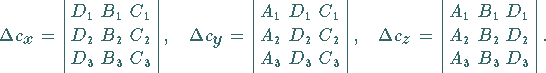 |
(3.406b) |
Drei Ebenen schneiden sich in einem Punkt, wenn 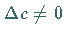 ist.
Ist
ist.
Ist 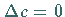 und wenigstens eine Unterdeterminante zweiter Ordnung
und wenigstens eine Unterdeterminante zweiter Ordnung 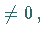 dann sind die Ebenen einer Geraden parallel; sind alle Unterdeterminanten
dann sind die Ebenen einer Geraden parallel; sind alle Unterdeterminanten 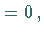 dann
gehen die Ebenen durch eine Gerade hindurch.
dann
gehen die Ebenen durch eine Gerade hindurch.
Parallelitäts- und Orthogonalitätsbedingung für Ebenen
1. Parallelitätsbedingung: Zwei Ebenen sind parallel, wenn gilt
 |
(3.407) |
2. Orthogonalitätsbedingung: Zwei Ebenen stehen senkrecht aufeinander, wenn
gilt
 |
(3.408) |
Schnittpunkt von vier Ebenen
Die Koordinaten des Schnittpunktes von vier Ebenen, gegeben durch die vier Gleichungen
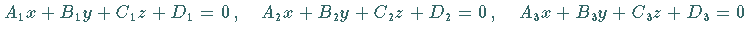 und
und
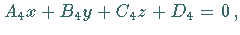 werden berechnet, indem zuerst der
Schnittpunkt dreier beliebiger Ebenen bestimmt wird.
In diesem Falle
werden berechnet, indem zuerst der
Schnittpunkt dreier beliebiger Ebenen bestimmt wird.
In diesem Falle 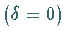 ist die vierte Gleichung eine Folge der übrigen drei
Gleichungen.
ist die vierte Gleichung eine Folge der übrigen drei
Gleichungen.
Vier Ebenen gehen dann und nur dann durch einen Punkt, wenn gilt:
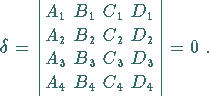 |
(3.409) |
Abstand zweier paralleler Ebenen
Wenn die Parallelitätsbedingung erfüllt ist und die Gleichungen
der Ebenen gegeben sind durch die Gleichungen
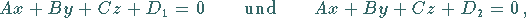 |
(3.410) |
dann beträgt der Abstand
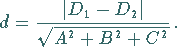 |
(3.411) |