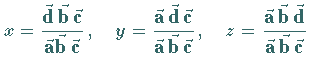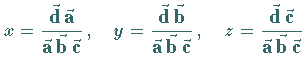| Gleichung |
Lösung |
1. 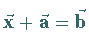 |
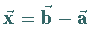 |
2. 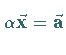 |
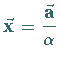 |
3. 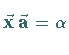 |
Die Gleichung ist unbestimmt; trägt man alle Vektoren 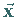 ,
die
dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte
auf einer Ebene, die auf dem Vektor ,
die
dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte
auf einer Ebene, die auf dem Vektor 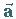 senkrecht steht.
Die Gleichung (3) nennt man die vektorielle Gleichung dieser
Ebene .
senkrecht steht.
Die Gleichung (3) nennt man die vektorielle Gleichung dieser
Ebene . |
4. 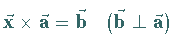 |
Die Gleichung ist unbestimmt; trägt man alle Vektoren 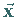 ,
die
dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte
auf einer dem Vektor ,
die
dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte
auf einer dem Vektor 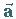 parallelen Geraden.
Die Gleichung (4) nennt man die vektorielle Gleichung dieser
Geraden .
parallelen Geraden.
Die Gleichung (4) nennt man die vektorielle Gleichung dieser
Geraden . |
5.
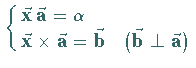 |
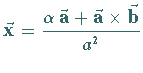 |
6. 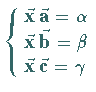 |
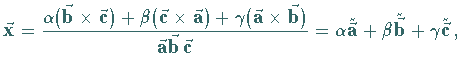 wobei
wobei 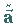 , ,
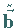 , ,
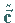 die zu
die zu
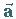 , ,
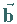 , ,
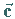 reziproken Vektoren sind (vgl.
reziproke Vektoren).
reziproken Vektoren sind (vgl.
reziproke Vektoren). |
7. 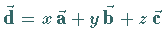 |
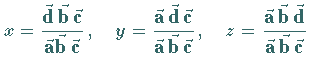 |
8.
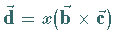
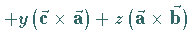 |
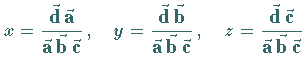
|
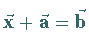
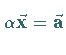
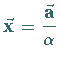
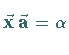
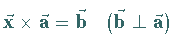
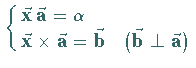
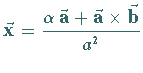
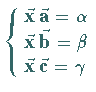
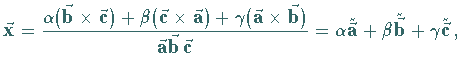 wobei
wobei