Themen dieser Seite
Gleichung einer Geraden im Raum, allgemeiner Fall
Da eine Gerade im Raum als Schnitt zweier Ebenen definiert werden kann, ist sie analytisch
durch ein System zweier linearer Gleichungen darstellbar.
a) In Komponentenschreibweise:
 |
(3.412a) |
b) in Vektorschreibweise:
 |
(3.412b) |
Gleichung der Geraden in zwei projizierenden Ebenen
Die zwei Gleichungen
 |
(3.413) |
definieren je eine Ebene, die durch die Gerade hindurchgehen und auf der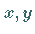 
- bzw.
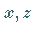-Ebene senkrecht stehen.
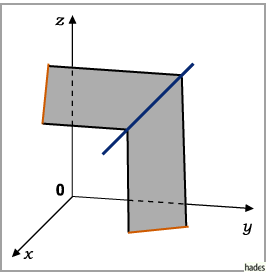
Man nennt sie projizierende Ebenen.
Auf Geraden, die parallel zur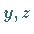 
-Ebene verlaufen, ist diese Form der Darstellung
nicht anwendbar, so daß hier die Projektionen auf ein anderes Koordinatenebenenpaar
zu beziehen sind.
Gleichung einer Geraden durch einen Punkt und parallel zum Richtungsvektor
Die Gleichung einer Geraden durch einen Punkt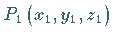 
und parallel
zu einem Richtungsvektor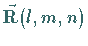 
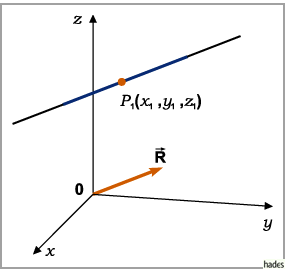
ergibt sich
a) in Komponentendarstellung
 |
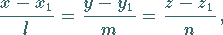(3.414a) |
b) in Vektordarstellung
 |
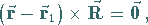(3.414b) |
c) in Parameterform
 |
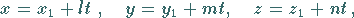(3.414c) |
d) in Vektorschreibweise
 |
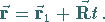(3.414d) |
Die Darstellung (3.414a) ergibt sich aus (3.412a) mit Hilfe von
 |
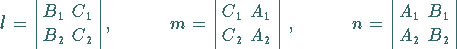(3.415a) |
oder in Vektorschreibweise
 |
(3.415b) |
wobei die Zahlen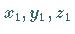 
so gewählt werden, daß die Gleichungen
(3.412a) erfüllt werden.
Gleichung einer Geraden durch zwei Punkte
Die Gleichung einer Geraden durch die zwei Punkte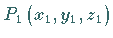 
und
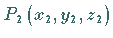
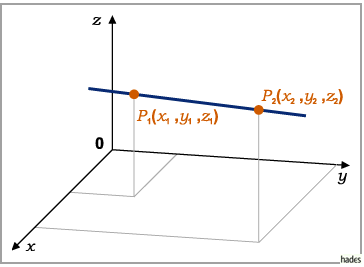
lautet in
a) Komponentenschreibweise
 |
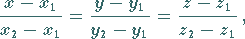(3.416a) |
b) Vektorschreibweise
 |
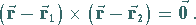(3.416b) |
(S. auch Produkte von Vektoren.)
Gleichung einer Geraden durch einen Punkt senkrecht zu einer Ebene
Der Punkt sei durch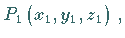 
die Ebene durch die Gleichung
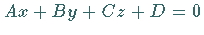oder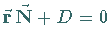 
gegeben.
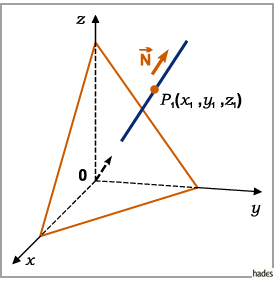
Die Gleichung einer Geraden durch einen Punkt senkrecht zu einer Ebene lautet dann in
a) Komponentenschreibweise
 |
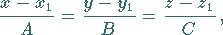(3.417a) |
b) Vektorschreibweise
 |
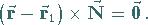(3.417b) |
(S. auch Produkte von Vektoren.)
