Themen dieser Seite
Gleichung einer Fläche
Jeder Gleichung
 |
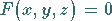(3.390) |
entspricht eine Fläche, deren Eigenschaft es ist, daß die Koordinaten jedes
beliebigen ihrer Punkte 
dieser Gleichung genügen.
Umgekehrt ist jeder Punkt, dessen Koordinaten der Gleichung genügen, ein Punkt auf
dieser Fläche.
Die Gleichung (3.390) wird die Gleichung dieser Fläche genannt.
Gleichung einer Zylinderfläche:
Die Gleichung einer Zylinderfläche
(s. auch Zylinderfläche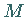 
), deren Erzeugende parallel zur
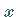-Achse verlaufen, enthält keine 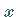-Koordinate: 
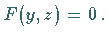Entsprechend enthalten die Gleichungen von Zylinderflächen, deren Erzeugende parallel
zur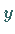 
- bzw. zur 
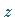-Achse verlaufen, keine 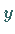- bzw. 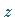-Koordinate: 
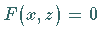bzw.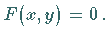 
Die Gleichung 
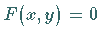beschreibt die Schnittkurve zwischen der Zylinderfläche und
der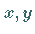 
-Ebene.
Wenn die Richtungskosinus oder ihnen proportionale Größen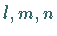 
der Erzeugenden
einer Zylinderfläche gegeben sind, dann hat die Gleichung die Form
 |
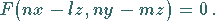(3.391) |
Gleichung einer Rotationsfläche:
Die Gleichung einer Rotationsfläche, d.h. einer Fläche, die durch Rotation einer
gegebenen Kurve in der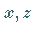 
-Ebene mit der Gleichung 
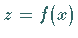erzeugt wird, ergibt
sich allgemein zu
 |
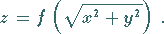(3.392) |
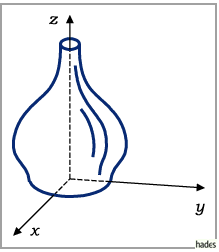
In Analogie dazu werden die Gleichungen von Flächen erhalten, die durch Rotation einer
gegebenen Kurve um eine andere Koordinate entstehen.
Die Gleichung einer Kegelfläche , deren Spitze im Koordinatenursprung liegt
(s. Kegel), ist von der Gestalt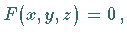 
wobei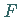 
eine homogene Funktion der Koordinaten ist (s. homogene Funktion).
