Polynominterpolation
Die Grundaufgabe der Interpolation besteht darin, durch eine Reihe von Punkten
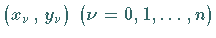eine geeignete Kurve
hindurchzulegen.
Graphisch geschieht das mit Hilfe eines Kurvenlineals, rechnerisch mit Hilfe einer
Funktion 
,
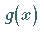die an den Stellen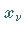 
,
den sogenannten Stützstellen ,
die gegebenen Werte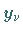 
als Funktionswerte annimmt, d.h., 
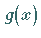erfüllt die
Interpolationsbedingung
 |
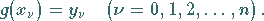(19.156) |
Als Interpolationsfunktionen sind in erster Linie Polynome gebräuchlich bzw. bei
periodischen Funktionen sogenannte trigonometrische Polynome.
Im letzteren Fall spricht man von
trigonometrischer Interpolation.
Werden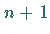 
Stützstellen benutzt, so heißt 
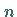die Ordnung der Interpolation, und
der Grad des Interpolationspolynoms ist dann höchstens gleich 
.
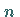Da mit zunehmendem Polynomgrad die Interpolationspolynome starke Oszillationen aufweisen,
die in der Regel unerwünscht sind, zerlegt man zweckmäßigerweise das
Interpolationsintervall in Teilintervalle und geht zur
Spline-Interpolation über.
