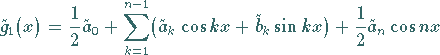|
|
|
|
und 
gebildet werden, haben wichtige Approximationseigenschaften.
Zwei davon sind:
.
Das spezielle trigonometrische Polynom
 |
(19.211) |
mit den Koeffizienten (19.210) erfüllt an den Stützstellen 
(19.209) die Interpolationsbedingung
 |
(19.212) |
Infolge der Periodizität von 
ist 
.
2. Approximation im Mittel: Es sei .
Das spezielle trigonometrische Polynom
 |
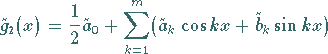(19.213) |
mit 
und den Koeffizienten (19.210) approximiert die Funktion
im
diskreten quadratischen Mittel bezüglich der 
Stützstellen
(19.209),
d.h., die Fehlerquadratsumme
Die Formeln (19.210) bilden den Ausgangspunkt für verschiedene Verfahren zur
effektiven Berechnung der FOURIER-Koeffizienten.
|
|
