In vielen praktischen Fällen wird das Interpolationspolynom 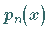 explizit nicht
benötigt, sondern nur sein Funktionswert an einer vorgegebenen Stelle
explizit nicht
benötigt, sondern nur sein Funktionswert an einer vorgegebenen Stelle 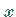 des
Interpolationsgebietes.
Zur Berechnung dieses Funktionswertes kann man nach AITKEN/NEVILLE rekursiv vorgehen.
Dazu verwendet man zweckmäßigerweise die Bezeichnung
des
Interpolationsgebietes.
Zur Berechnung dieses Funktionswertes kann man nach AITKEN/NEVILLE rekursiv vorgehen.
Dazu verwendet man zweckmäßigerweise die Bezeichnung
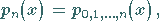 |
(19.161) |
in der die Indizierung die verwendeten Stützstellen und damit auch den Grad des
Interpolationspolynoms angibt.
Es gilt
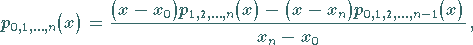 |
(19.162) |
d.h., der Funktionswert 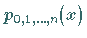 ergibt sich durch lineare Interpolation
aus den Funktionswerten von
ergibt sich durch lineare Interpolation
aus den Funktionswerten von 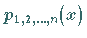 und
und 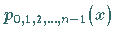 ,
zwei Interpolationspolynomen vom Grad
,
zwei Interpolationspolynomen vom Grad 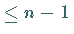 .
Die gezielte Anwendung von (19.162) führt auf ein Schema, das für den Fall
.
Die gezielte Anwendung von (19.162) führt auf ein Schema, das für den Fall
 angegeben werden soll:
angegeben werden soll:
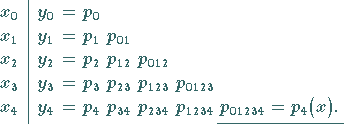 |
(19.163) |
Die Elemente von (19.163) werden spaltenweise berechnet.
Ein neuer Wert im Schema entsteht jeweils aus dem links daneben stehenden und dem
unmittelbar über diesem stehenden Wert, z.B.
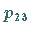 |
 |
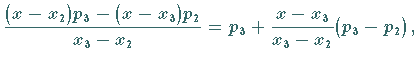 |
(19.164a) |
 |
 |
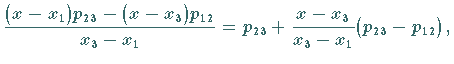 |
(19.164b) |
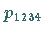 |
 |
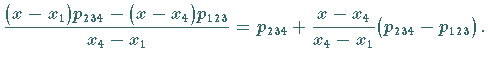 |
(19.164c) |
Für die Durchführung des Algorithmus von AITKEN/NEVILLE auf dem Computer
braucht man nach Lit. 19.3 nur einen Vektor  mit
mit 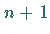 Komponenten, der
nacheinander die einzelnen Spalten von (19.163) aufnimmt.
Dazu wird vereinbart, daß der Wert
Komponenten, der
nacheinander die einzelnen Spalten von (19.163) aufnimmt.
Dazu wird vereinbart, daß der Wert
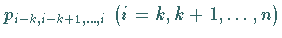 der
der 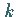 -ten Spalte die
-ten Spalte die 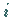 -te
Komponente
-te
Komponente 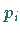 von
von  wird.
Damit sind die Spalten von (19.163) von oben nach unten zu berechnen, um die noch
benötigten Werte zur Verfügung zu haben.
Der Algorithmus besteht dann aus folgenden zwei Schritten:
wird.
Damit sind die Spalten von (19.163) von oben nach unten zu berechnen, um die noch
benötigten Werte zur Verfügung zu haben.
Der Algorithmus besteht dann aus folgenden zwei Schritten:
Nach Abschluß von (19.165b) stellt 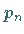 den gesuchten Funktionswert von
den gesuchten Funktionswert von
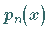 an der Stelle
an der Stelle 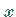 dar.
dar.
![]() mit
mit ![]() Komponenten, der
nacheinander die einzelnen Spalten von (19.163) aufnimmt.
Dazu wird vereinbart, daß der Wert
Komponenten, der
nacheinander die einzelnen Spalten von (19.163) aufnimmt.
Dazu wird vereinbart, daß der Wert
![]() der
der ![]() -ten Spalte die
-ten Spalte die ![]() -te
Komponente
-te
Komponente ![]() von
von ![]() wird.
Damit sind die Spalten von (19.163) von oben nach unten zu berechnen, um die noch
benötigten Werte zur Verfügung zu haben.
Der Algorithmus besteht dann aus folgenden zwei Schritten:
wird.
Damit sind die Spalten von (19.163) von oben nach unten zu berechnen, um die noch
benötigten Werte zur Verfügung zu haben.
Der Algorithmus besteht dann aus folgenden zwei Schritten: