Numerische Lösung von Gleichungssystemen
Bei vielen praktischen Aufgaben werden für 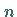 unbekannte Größen
unbekannte Größen
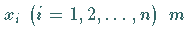 Bedingungen in Gleichungsform gestellt:
Bedingungen in Gleichungsform gestellt:
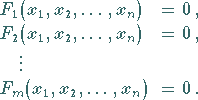 |
(19.23) |
Die Unbekannten 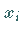 sind so zu bestimmen, daß sie eine Lösung des
Gleichungssystems (19.23) darstellen.
In der Regel ist
sind so zu bestimmen, daß sie eine Lösung des
Gleichungssystems (19.23) darstellen.
In der Regel ist 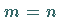 ,
d.h., die Anzahl der Unbekannten stimmt mit der Anzahl der
Gleichungen überein.
Im Falle
,
d.h., die Anzahl der Unbekannten stimmt mit der Anzahl der
Gleichungen überein.
Im Falle 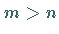 bezeichnet man (19.23) als überbestimmtes System ,
im Falle
bezeichnet man (19.23) als überbestimmtes System ,
im Falle 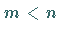 als unterbestimmtes System .
als unterbestimmtes System .
Überbestimmte Systeme haben in der Regel keine Lösung.
Man formuliert deshalb die zu (19.23) gehörende Quadratmittelaufgabe
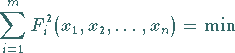 |
(19.24) |
als Ersatzaufgabe.
Im unterbestimmten Fall können im allgemeinen 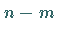 Unbekannte frei gewählt werden,
so daß die Lösung von (19.23) von
Unbekannte frei gewählt werden,
so daß die Lösung von (19.23) von 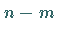 Parametern abhängt.
Man spricht dann von einer
Parametern abhängt.
Man spricht dann von einer 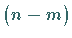 -dimensionalen Lösungsmannigfaltigkeit .
-dimensionalen Lösungsmannigfaltigkeit .
Man unterscheidet lineare und nichtlineare Gleichungssysteme , je nachdem, ob
in (19.23) die Unbekannten nur linear oder auch nichtlinear auftreten.