Newton-Verfahren
Das NEWTON-Verfahren geht von der Nullstellenaufgabe (19.55) aus.
Nach Vorgabe von geschätzten Näherungswerten
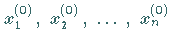werden die Funktionen 
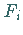als
Funktionen von 
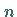unabhängigen Variablen 
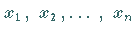nach
TAYLOR entwickelt.
Durch Abbruch dieser Entwicklungen nach den linearen Gliedern erhält man aus
(19.55) ein lineares Gleichungssystem, mit dessen Hilfe man iterativ
Verbesserungen nach folgender Vorschrift ermitteln kann:
Die Koeffizientenmatrix des linearen Gleichungssystems (19.61), das in jedem
Iterationsschritt zu lösen ist, lautet
 |
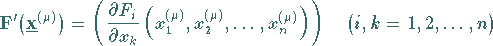(19.62) |
und wird als JACOBI-Matrix bezeichnet.
Das NEWTON-Verfahren ist lokal quadratisch konvergent, d.h.,
seine schnelle Konvergenz ist wesentlich von der Güte der Startnäherungen abhängig.
Setzt man in (19.61)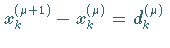 
,
dann
kann das NEWTON-Verfahren in der Korrekturform
 |
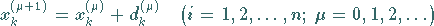(19.63) |
geschrieben werden.
Zur Herabsetzung der Startwertempfindlichkeit kann man dann analog zum
Relaxationsverfahren einen sogenannten Dämpfungs- oder
Schrittweitenparameter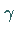 
einführen:
 |
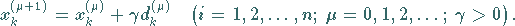(19.64) |
Angaben zur Bestimmung von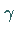
findet man in Lit. 19.27.
