Cholesky-Verfahren bei symmetrischer Koeffizientenmatrix
In vielen Fällen ist in (19.26) die Koeffizientenmatrix 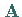 nicht nur symmetrisch, sondern auch positiv definit , d.h., für die zugehörige
quadratische Form
nicht nur symmetrisch, sondern auch positiv definit , d.h., für die zugehörige
quadratische Form 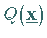 gilt:
gilt:
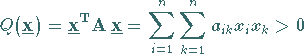 |
(19.34) |
für alle 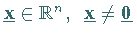 .
Da es zu jeder symmetrischen positiv definiten Matrix
.
Da es zu jeder symmetrischen positiv definiten Matrix  eine eindeutige
Dreieckszerlegung
eine eindeutige
Dreieckszerlegung
 |
(19.35) |
mit
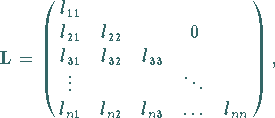 |
(19.36a) |
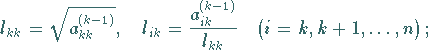 |
(19.36b) |
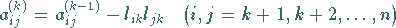 |
(19.36c) |
gibt, kann die Lösung des zugehörigen linearen Gleichungssystems
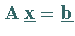 nach dem CHOLESKY- Verfahren in folgenden
Schritten durchgeführt werden:
nach dem CHOLESKY- Verfahren in folgenden
Schritten durchgeführt werden:
1.  :
Ermittlung der sogenannten
CHOLESKY-Zerlegung und Substitution
:
Ermittlung der sogenannten
CHOLESKY-Zerlegung und Substitution 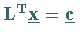 .
.
2. 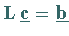 :
Bestimmung des Hilfsvektors
:
Bestimmung des Hilfsvektors 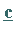 durch
Vorwärtseinsetzen.
durch
Vorwärtseinsetzen.
3. 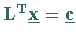 :
Bestimmung der Lösung
:
Bestimmung der Lösung 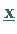 durch
Rückwärtseinsetzen.
durch
Rückwärtseinsetzen.
Für große Werte von 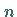 ist der Aufwand beim CHOLESKY-Verfahren etwa halb so
groß wie bei der LR-Zerlegung gemäß (19.31).
ist der Aufwand beim CHOLESKY-Verfahren etwa halb so
groß wie bei der LR-Zerlegung gemäß (19.31).
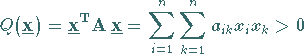
![]() .
Da es zu jeder symmetrischen positiv definiten Matrix
.
Da es zu jeder symmetrischen positiv definiten Matrix ![]() eine eindeutige
Dreieckszerlegung
eine eindeutige
Dreieckszerlegung
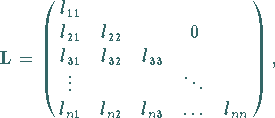
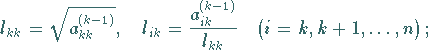
![]() nach dem CHOLESKY- Verfahren in folgenden
Schritten durchgeführt werden:
nach dem CHOLESKY- Verfahren in folgenden
Schritten durchgeführt werden:
![]() :
Ermittlung der sogenannten
CHOLESKY-Zerlegung und Substitution
:
Ermittlung der sogenannten
CHOLESKY-Zerlegung und Substitution ![]() .
.
![]() :
Bestimmung des Hilfsvektors
:
Bestimmung des Hilfsvektors ![]() durch
Vorwärtseinsetzen.
durch
Vorwärtseinsetzen.
![]() :
Bestimmung der Lösung
:
Bestimmung der Lösung ![]() durch
Rückwärtseinsetzen.
durch
Rückwärtseinsetzen.
![]() ist der Aufwand beim CHOLESKY-Verfahren etwa halb so
groß wie bei der LR-Zerlegung gemäß (19.31).
ist der Aufwand beim CHOLESKY-Verfahren etwa halb so
groß wie bei der LR-Zerlegung gemäß (19.31).