Ableitungsfreies Gauß-Newton-Verfahren
Zur Lösung der Quadratmittelaufgabe (19.24) geht man im
nichtlinearen Fall ( nichtlineare Ausgleichsaufgabe ) iterativ wie folgt vor:
1. Ausgehend von geeigneten Startnäherungen
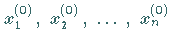 approximiert man wie beim
NEWTON-Verfahren (dort gemäß (19.61)), die nichtlinearen
Funktionen
approximiert man wie beim
NEWTON-Verfahren (dort gemäß (19.61)), die nichtlinearen
Funktionen 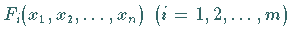 durch lineare
Näherungen
durch lineare
Näherungen 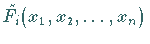 ,
die in jedem Iterationsschritt
gemäß
,
die in jedem Iterationsschritt
gemäß
berechnet werden.
2. Man setzt in (19.65) 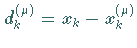 und
ermittelt die Verbesserungen
und
ermittelt die Verbesserungen 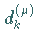 nach der GAUSSschen
Fehlerquadratmethode, d.h. durch Lösung der linearen Quadratmittelaufgabe
nach der GAUSSschen
Fehlerquadratmethode, d.h. durch Lösung der linearen Quadratmittelaufgabe
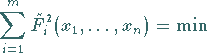 |
(19.66) |
z.B. mit Hilfe der Normalgleichungen (19.42), oder des
HOUSEHOLDER-Verfahrens.
3. Man erhält Näherungen für die gesuchte Lösung durch
wobei 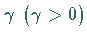 ein Schrittweitenparameter wie beim
NEWTON-Verfahren ist.
ein Schrittweitenparameter wie beim
NEWTON-Verfahren ist.
Durch Wiederholung der Schritte 2 und 3 mit 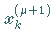 an Stelle von
an Stelle von
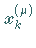 erhält man das GAUSS-NEWTON- Verfahren .
Es liefert eine Folge von Näherungswerten, deren Konvergenz sehr stark von der Güte
der Startnäherungen abhängt.
Mit Hilfe des Schrittweitenparameters
erhält man das GAUSS-NEWTON- Verfahren .
Es liefert eine Folge von Näherungswerten, deren Konvergenz sehr stark von der Güte
der Startnäherungen abhängt.
Mit Hilfe des Schrittweitenparameters 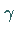 läßt sich jedoch ein sogenannter
Abstieg , d.h. eine Verkleinerung der Fehlerquadratsumme, erzielen.
läßt sich jedoch ein sogenannter
Abstieg , d.h. eine Verkleinerung der Fehlerquadratsumme, erzielen.
Wenn die Berechnung der partiellen Ableitungen
mit großem Aufwand verbunden ist, kann man die partiellen Ableitungen durch
Differenzenquotienten sehr einfach approximieren:
| |
|
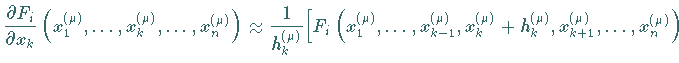 |
|
| |
|
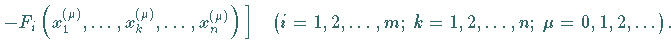 |
(19.68) |
Die sogenannten Diskretisierungsschrittweiten 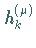 können in
Abhängigkeit von Iterationsschritt und Variablen speziell gewählt werden.
können in
Abhängigkeit von Iterationsschritt und Variablen speziell gewählt werden.
Verwendet man die Näherungen (19.68), dann müssen bei der Durchführung des
GAUSS-NEWTON-Verfahrens nur Funktionswerte 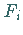 berechnet werden, d.h., das
Verfahren ist dann ableitungsfrei .
berechnet werden, d.h., das
Verfahren ist dann ableitungsfrei .
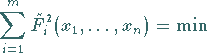
![]() ein Schrittweitenparameter wie beim
NEWTON-Verfahren ist.
ein Schrittweitenparameter wie beim
NEWTON-Verfahren ist.
![]() an Stelle von
an Stelle von
![]() erhält man das GAUSS-NEWTON- Verfahren .
Es liefert eine Folge von Näherungswerten, deren Konvergenz sehr stark von der Güte
der Startnäherungen abhängt.
Mit Hilfe des Schrittweitenparameters
erhält man das GAUSS-NEWTON- Verfahren .
Es liefert eine Folge von Näherungswerten, deren Konvergenz sehr stark von der Güte
der Startnäherungen abhängt.
Mit Hilfe des Schrittweitenparameters ![]() läßt sich jedoch ein sogenannter
Abstieg , d.h. eine Verkleinerung der Fehlerquadratsumme, erzielen.
läßt sich jedoch ein sogenannter
Abstieg , d.h. eine Verkleinerung der Fehlerquadratsumme, erzielen.