Themen dieser Seite
Vom Torus zum Chaos
Hopf-Landau-Modell der Turbulenz
Die Frage des Übergangs von einem regulären laminaren Verhalten
zu einem irregulären turbulenten Verhalten ist besonders für
Systeme mit verteilten Parametern, die z.B. durch partielle Differentialgleichungen
beschrieben werden, von Interesse.
Aus dieser Sicht läßt sich Chaos als zeitlich irreguläres, aber räumlich
geordnetes Verhalten interpretieren.
Turbulenz dagegen ist ein Systemverhalten, das sowohl zeitlich als auch räumlich
irregulär ist.
Das HOPF- LANDAU-Modell erklärt die Entstehung der Turbulenz über
eine unendliche Kaskade von HOPF-Bifurkationen:
Bei 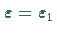 entsteht aus einer Ruhelage ein Grenzzyklus, der bei
entsteht aus einer Ruhelage ein Grenzzyklus, der bei
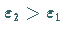 instabil wird und zu einem Torus
instabil wird und zu einem Torus 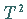 führt.
Bei der
führt.
Bei der 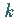 -ten Bifurkation entsteht ein
-ten Bifurkation entsteht ein 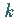 -dimensionaler Torus, der durch nicht
geschlossene Orbits aufgewickelt wird.
Das HOPF- LANDAU-Modell führt i. allg. nicht zu einem Attraktor, der durch
sensitive Abhängigkeit von den Anfangsbedingungen und Durchmischung gekennzeichnet ist.
Im System (17.53) sei
-dimensionaler Torus, der durch nicht
geschlossene Orbits aufgewickelt wird.
Das HOPF- LANDAU-Modell führt i. allg. nicht zu einem Attraktor, der durch
sensitive Abhängigkeit von den Anfangsbedingungen und Durchmischung gekennzeichnet ist.
Im System (17.53) sei 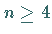 und
und 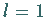 .
Bei Änderung des Parameters
.
Bei Änderung des Parameters 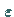 sei die Bifurkationssequenz Ruhelage
sei die Bifurkationssequenz Ruhelage 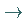 Periodischer Orbit
Periodischer Orbit 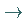 Torus
Torus 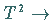 Torus
Torus 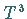 über drei aufeinander folgende
HOPF-Bifurkationen realisiert.
über drei aufeinander folgende
HOPF-Bifurkationen realisiert.
Der auf 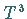 gegebene quasiperiodische Fluß sei strukturell instabil.
Dann können schon bestimmte kleine Störungen von (17.53)
zum Zerfall von
gegebene quasiperiodische Fluß sei strukturell instabil.
Dann können schon bestimmte kleine Störungen von (17.53)
zum Zerfall von 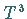 und zur Bildung eines seltsamen Attraktors führen, der
strukturell stabil ist.
Gegeben sei das hinreichend glatte System (17.53) bei
und zur Bildung eines seltsamen Attraktors führen, der
strukturell stabil ist.
Gegeben sei das hinreichend glatte System (17.53) bei 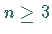 und
und 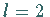 .
Beim Parameterwert
.
Beim Parameterwert 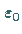 habe System (17.53) einen
anziehenden glatten Torus
habe System (17.53) einen
anziehenden glatten Torus 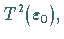 der aufgespannt wird durch einen stabilen
periodischen Orbit
der aufgespannt wird durch einen stabilen
periodischen Orbit 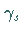 ,
einen sattelartigen periodischen Orbit
,
einen sattelartigen periodischen Orbit 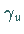 und
dessen instabile Mannigfaltigkeit
und
dessen instabile Mannigfaltigkeit 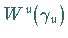 ( Resonanz-Torus ).
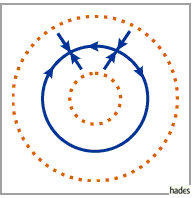
Die invarianten Mannigfaltigkeiten der Ruhelagen der
POINCARÉ-Abbildung bezüglich einer Fläche, die
transversal zur Längsrichtung den Torus schneidet, sind in der folgenden Abbildung zu
sehen.
( Resonanz-Torus ).
Die invarianten Mannigfaltigkeiten der Ruhelagen der
POINCARÉ-Abbildung bezüglich einer Fläche, die
transversal zur Längsrichtung den Torus schneidet, sind in der folgenden Abbildung zu
sehen.
Der Multiplikator 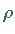 von
von 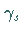 ,
der dem Einheitskreis am nächsten liegt, sei
reell und einfach.
Es sei weiter
,
der dem Einheitskreis am nächsten liegt, sei
reell und einfach.
Es sei weiter 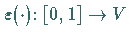 eine beliebige stetige
Kurve im Parameterraum, für die
eine beliebige stetige
Kurve im Parameterraum, für die 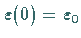 gilt, und für die
das System (17.53) bei
gilt, und für die
das System (17.53) bei 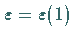 keinen
invarianten Resonanz-Torus besitzt.
Dann gelten folgende Aussagen:
keinen
invarianten Resonanz-Torus besitzt.
Dann gelten folgende Aussagen:
a) Es existiert ein Wert 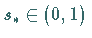 ,
bei dem
,
bei dem  seine Glattheit verliert .
Dabei wird entweder der Multiplikator
seine Glattheit verliert .
Dabei wird entweder der Multiplikator 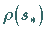 komplex, oder die instabile
Mannigfaltigkeit
komplex, oder die instabile
Mannigfaltigkeit 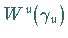 verliert ihre Glattheit nahe
verliert ihre Glattheit nahe 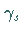 .
.
b) Es existiert ein weiterer Parameterwert 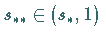 ,
so daß
das System (17.53) für
,
so daß
das System (17.53) für 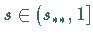 keinen resonanten Torus besitzt.
Der Torus zerfällt dabei nach einem der folgenden Szenarien:
keinen resonanten Torus besitzt.
Der Torus zerfällt dabei nach einem der folgenden Szenarien:
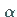 ) Der periodische Orbit
) Der periodische Orbit 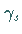 verliert seine Stabilität bei
verliert seine Stabilität bei
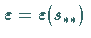 .
Es kommt zu einer lokalen Bifurkation wie der Periodenverdopplung oder der Abspaltung
eines Torus.
.
Es kommt zu einer lokalen Bifurkation wie der Periodenverdopplung oder der Abspaltung
eines Torus.
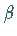 ) Die periodischen Orbits
) Die periodischen Orbits 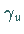 und
und 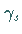 fallen bei
fallen bei
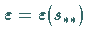 zusammen (Sattelknoten-Bifurkation) und heben
sich dabei auf.
zusammen (Sattelknoten-Bifurkation) und heben
sich dabei auf.
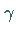 ) Die stabilen und instabilen Mannigfaltigkeiten von
) Die stabilen und instabilen Mannigfaltigkeiten von 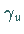 schneiden
sich bei
schneiden
sich bei 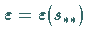 nicht transversal
(s. Bifurkationsdiagramm in der folgenden Abbildung).
nicht transversal
(s. Bifurkationsdiagramm in der folgenden Abbildung).
Die Punkte auf der schnabelförmigen Kurve 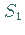 entsprechen dem Verschmelzen von
entsprechen dem Verschmelzen von
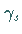 und
und 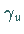 (Sattelknoten-Bifurkation).
Die Schnabelspitze
(Sattelknoten-Bifurkation).
Die Schnabelspitze 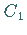 liegt auf einer Kurve
liegt auf einer Kurve 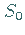 ,
die der Abspaltung eines Torus
entspricht.
,
die der Abspaltung eines Torus
entspricht.
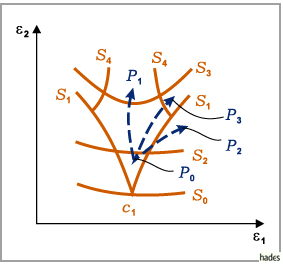
Auf der Kurve 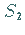 liegen die Parameterpunkte, bei denen ein Glattheitsverlust eintritt,
während die Punkte auf
liegen die Parameterpunkte, bei denen ein Glattheitsverlust eintritt,
während die Punkte auf 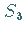 die Auflösung eines
die Auflösung eines 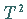 -Torus charakterisieren.
Auf
-Torus charakterisieren.
Auf 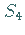 liegen die Parameterpunkte, für die sich stabile und instabile
Mannigfaltigkeiten von
liegen die Parameterpunkte, für die sich stabile und instabile
Mannigfaltigkeiten von 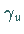 nicht transversal schneiden.
Sei
nicht transversal schneiden.
Sei 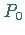 ein beliebiger Punkt in der Schnabelspitze, so daß bei diesem Parameterwert
ein Resonanz-Torus
ein beliebiger Punkt in der Schnabelspitze, so daß bei diesem Parameterwert
ein Resonanz-Torus 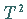 vorliegt.
Der Übergang von
vorliegt.
Der Übergang von 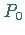 nach
nach 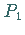 entspricht dem Fall
entspricht dem Fall
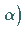 des Satzes.
Wird dabei auf
des Satzes.
Wird dabei auf 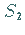 der Multiplikator
der Multiplikator 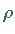 zu
zu 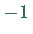 ,
so findet eine
Periodenverdopplung statt.
Eine sich anschließende Kaskade von weiteren Periodenverdopplungen kann zum Entstehen
eines seltsamen Attraktors führen.
Trifft beim Überqueren von
,
so findet eine
Periodenverdopplung statt.
Eine sich anschließende Kaskade von weiteren Periodenverdopplungen kann zum Entstehen
eines seltsamen Attraktors führen.
Trifft beim Überqueren von 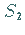 ein Paar konjugiert komplexer Multiplikatoren
ein Paar konjugiert komplexer Multiplikatoren
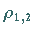 auf den Einheitskreis, dann kann es zur Abspaltung eines weiteren Torus
kommen, für den der Satz von AFRAIMOVICH und SHILNIKOV erneut anwendbar
ist.
auf den Einheitskreis, dann kann es zur Abspaltung eines weiteren Torus
kommen, für den der Satz von AFRAIMOVICH und SHILNIKOV erneut anwendbar
ist.
Der Übergang von 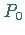 nach
nach 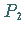 repräsentiert den Fall
repräsentiert den Fall
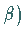 des Satzes:
Der Torus verliert die Glattheit, und beim Überqueren von
des Satzes:
Der Torus verliert die Glattheit, und beim Überqueren von 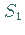 findet eine
Sattelknoten-Bifurkation statt.
Der Torus zerfällt, und ein Übergang zum Chaos über Intermittenz kann stattfinden.
findet eine
Sattelknoten-Bifurkation statt.
Der Torus zerfällt, und ein Übergang zum Chaos über Intermittenz kann stattfinden.
Der Übergang von 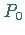 nach
nach 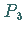 schließlich entspricht Fall
schließlich entspricht Fall
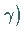 :
Nach dem Verlust der Glattheit bildet sich beim Überqueren von
:
Nach dem Verlust der Glattheit bildet sich beim Überqueren von 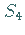 eine nicht robuste
homokline Kurve.
Der stabile Zyklus
eine nicht robuste
homokline Kurve.
Der stabile Zyklus 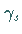 bleibt, und es entsteht eine zunächst nicht anziehende
hyperbolische Menge.
Wenn
bleibt, und es entsteht eine zunächst nicht anziehende
hyperbolische Menge.
Wenn 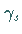 verschwindet, kann aus dieser Menge ein seltsamer Attraktor entstehen.
verschwindet, kann aus dieser Menge ein seltsamer Attraktor entstehen.
![]() nach
nach ![]() repräsentiert den Fall
repräsentiert den Fall
![]() des Satzes:
Der Torus verliert die Glattheit, und beim Überqueren von
des Satzes:
Der Torus verliert die Glattheit, und beim Überqueren von ![]() findet eine
Sattelknoten-Bifurkation statt.
Der Torus zerfällt, und ein Übergang zum Chaos über Intermittenz kann stattfinden.
findet eine
Sattelknoten-Bifurkation statt.
Der Torus zerfällt, und ein Übergang zum Chaos über Intermittenz kann stattfinden.
![]() nach
nach ![]() schließlich entspricht Fall
schließlich entspricht Fall
![]() :
Nach dem Verlust der Glattheit bildet sich beim Überqueren von
:
Nach dem Verlust der Glattheit bildet sich beim Überqueren von ![]() eine nicht robuste
homokline Kurve.
Der stabile Zyklus
eine nicht robuste
homokline Kurve.
Der stabile Zyklus ![]() bleibt, und es entsteht eine zunächst nicht anziehende
hyperbolische Menge.
Wenn
bleibt, und es entsteht eine zunächst nicht anziehende
hyperbolische Menge.
Wenn ![]() verschwindet, kann aus dieser Menge ein seltsamer Attraktor entstehen.
verschwindet, kann aus dieser Menge ein seltsamer Attraktor entstehen.