Intermittenz
Gegeben sei ein stabiler periodischer Orbit von (17.53), der bei
 seine Stabilität verliert, indem genau einer der Multiplikatoren,
die innerhalb des Einheitskreises lagen, den Wert
seine Stabilität verliert, indem genau einer der Multiplikatoren,
die innerhalb des Einheitskreises lagen, den Wert 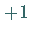 annimmt.
Nach dem Satz über die Zentrumsmannigfaltigkeit läßt
sich die entsprechende Sattelknoten-Bifurkation der
POINCARÉ-Abbildung durch eine eindimensionale Abbildung in
der Normalform
beschreiben.
Dabei ist
annimmt.
Nach dem Satz über die Zentrumsmannigfaltigkeit läßt
sich die entsprechende Sattelknoten-Bifurkation der
POINCARÉ-Abbildung durch eine eindimensionale Abbildung in
der Normalform
beschreiben.
Dabei ist 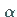 ein Parameter, für den
ein Parameter, für den 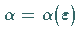 mit
mit
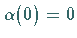 gilt.
Für positives
gilt.
Für positives 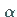 ist der Graph von
ist der Graph von 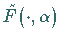 in der folgenden
Abbildung zu sehen.
in der folgenden
Abbildung zu sehen.
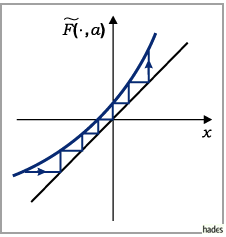
Wie die Abbildung zeigt, verweilen für 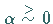 die Iterierten von
die Iterierten von
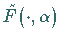 relativ lange in der Tunnelzone.
Für die Differentialgleichung (17.53) bedeutet dies, daß die entsprechenden
Orbits relativ lange in der Umgebung des ursprünglichen periodischen Orbits bleiben.
In dieser Zeit ist das Verhalten von (17.54) nahezu periodisch ( laminare
Phase ).
Ist die Tunnelzone durchlaufen, entflieht der betrachtete Orbit, was zu irregulären
Bewegungen führt ( turbulente Phase ).
Nach einem gewissen Zeitraum wird der Orbit eingefangen und erneut eine laminare Phase
eingeleitet.
Ein seltsamer Attraktor entsteht in der beschriebenen Situation dann, wenn der periodische
Orbit verschwindet und seine Stabilität an die chaotische Menge vererbt.
Die Sattelknoten-Bifurkation ist nur eine der generischen lokalen Bifurkationen, die im
Intermittenz-Szenario eine Rolle spielen.
Zwei weitere sind die Periodenverdopplung und die Abspaltung eines Torus.
relativ lange in der Tunnelzone.
Für die Differentialgleichung (17.53) bedeutet dies, daß die entsprechenden
Orbits relativ lange in der Umgebung des ursprünglichen periodischen Orbits bleiben.
In dieser Zeit ist das Verhalten von (17.54) nahezu periodisch ( laminare
Phase ).
Ist die Tunnelzone durchlaufen, entflieht der betrachtete Orbit, was zu irregulären
Bewegungen führt ( turbulente Phase ).
Nach einem gewissen Zeitraum wird der Orbit eingefangen und erneut eine laminare Phase
eingeleitet.
Ein seltsamer Attraktor entsteht in der beschriebenen Situation dann, wenn der periodische
Orbit verschwindet und seine Stabilität an die chaotische Menge vererbt.
Die Sattelknoten-Bifurkation ist nur eine der generischen lokalen Bifurkationen, die im
Intermittenz-Szenario eine Rolle spielen.
Zwei weitere sind die Periodenverdopplung und die Abspaltung eines Torus.