Themen dieser Seite
Die FOURIER-Transformation ist eine Integraltransformation der Form
(15.1a), die aus dem FOURIER-Integral (15.64b) dadurch
entsteht, daß man
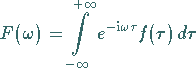 |
(15.70) |
substituiert.
Damit erhält man den folgenden Zusammenhang zwischen der reellen Originalfunktion 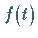 und der im allgemeinen komplexen Bildfunktion
und der im allgemeinen komplexen Bildfunktion 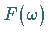 :
:
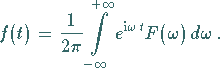 |
(15.71) |
In der Kurzschreibweise verwendet man das Zeichen 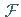 :
:
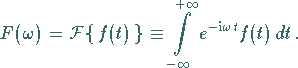 |
(15.72) |
Die Originalfunktion 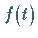 heißt FOURIER-transformierbar, wenn das Integral
(15.70), also ein uneigentliches Integral mit dem Parameter
heißt FOURIER-transformierbar, wenn das Integral
(15.70), also ein uneigentliches Integral mit dem Parameter 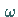 existiert.
Wenn das FOURIER-Integral nicht als gewöhnliches uneigentliches Integral
existiert, ist es als CAUCHYscher Hauptwert zu verstehen.
Die Bildfunktion
existiert.
Wenn das FOURIER-Integral nicht als gewöhnliches uneigentliches Integral
existiert, ist es als CAUCHYscher Hauptwert zu verstehen.
Die Bildfunktion 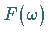 nennt man auch FOURIER-Transformierte ; sie
ist beschränkt, stetig und strebt für
nennt man auch FOURIER-Transformierte ; sie
ist beschränkt, stetig und strebt für 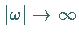 gegen Null:
gegen Null:
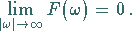 |
(15.73) |
Existenz und Beschränktheit von 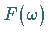 folgen direkt aus der offensichtlich
gültigen Ungleichung
folgen direkt aus der offensichtlich
gültigen Ungleichung
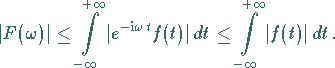 |
(15.74) |
Für die Stetigkeit von 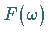 und die Eigenschaft
und die Eigenschaft 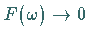 für
für
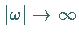 ist die Existenz der FOURIER-Transformierten eine
hinreichende Bedingung.
Diese Aussage wird häufig in folgender Form benutzt:
Wenn die Funktion
ist die Existenz der FOURIER-Transformierten eine
hinreichende Bedingung.
Diese Aussage wird häufig in folgender Form benutzt:
Wenn die Funktion 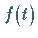 in
in 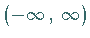 absolut integrierbar ist, dann ist
ihre FOURIER-Transformierte eine stetige Funktion von
absolut integrierbar ist, dann ist
ihre FOURIER-Transformierte eine stetige Funktion von 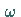 ,
und es gilt
(15.73).
Folgende Funktionen sind nicht FOURIER-transformierbar: konstante Funktionen,
beliebige periodische Funktionen (z.B.
,
und es gilt
(15.73).
Folgende Funktionen sind nicht FOURIER-transformierbar: konstante Funktionen,
beliebige periodische Funktionen (z.B. 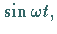
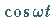 ),
Potenzfunktionen, Polynome, Exponentialfunktionen (z.B.
),
Potenzfunktionen, Polynome, Exponentialfunktionen (z.B. 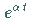 ,
Hyperbelfunktionen).
,
Hyperbelfunktionen).