1. Rechts offenes oder abgeschlossenes Definitionsintervall
Die Definition des uneigentlichen Integrals für eine Funktion 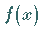 ,
die
ein rechts offenes Definitionsintervall
,
die
ein rechts offenes Definitionsintervall 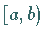 oder ein abgeschlossenes
Definitionsintervall
oder ein abgeschlossenes
Definitionsintervall 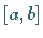 besitzt, aber im Punkt
besitzt, aber im Punkt 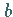 den Grenzwert
den Grenzwert
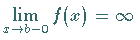 hat, lautet in beiden Fällen:
hat, lautet in beiden Fällen:
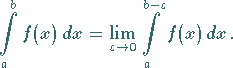 |
(8.85) |
Wenn dieser Grenzwert existiert, dann existiert bzw. konvergiert auch das Integral
und man spricht von einem konvergenten uneigentlichen Integral .
Existiert der Grenzwert nicht, dann existiert bzw. konvergiert auch das Integral nicht,
und man spricht von einem divergenten uneigentlichen Integral .
2. Links offenes oder abgeschlossenes Definitionsintervall
Die Definition des uneigentlichen Integrals für eine Funktion 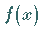 ,
die ein
links offenes Definitionsintervall
,
die ein
links offenes Definitionsintervall 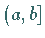 oder ein abgeschlossenes Definitionsintervall
oder ein abgeschlossenes Definitionsintervall
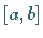 besitzt, aber im Punkt
besitzt, aber im Punkt 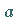 den Grenzwert
den Grenzwert
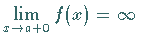 ,
erfolgt in Analogie zur Definition (8.85):
,
erfolgt in Analogie zur Definition (8.85):
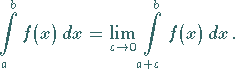 |
(8.86) |
3. Zwei halboffene angrenzende Definitionsintervalle
Die Definition des uneigentlichen Integrals für eine Funktion 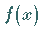 ,
die im
gesamten Intervall
,
die im
gesamten Intervall 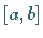 definiert ist, ausgenommen einen inneren Punkt
definiert ist, ausgenommen einen inneren Punkt 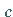 mit
mit
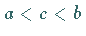 ,
d.h., für eine Funktion
,
d.h., für eine Funktion 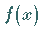 ,
die in zwei angrenzenden halboffenen
Intervallen
,
die in zwei angrenzenden halboffenen
Intervallen 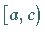 und
und 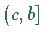 definiert ist, aber im Punkt
definiert ist, aber im Punkt 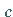 nicht beschränkt ist,
lautet:
nicht beschränkt ist,
lautet:
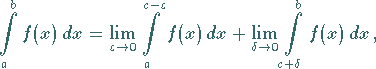 |
(8.87a) |
Dabei streben die Zahlen 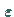 und
und 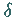 unabhängig voneinander gegen Null.
Wenn der Grenzwert (8.87a) nicht existiert, wohl aber
unabhängig voneinander gegen Null.
Wenn der Grenzwert (8.87a) nicht existiert, wohl aber
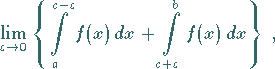 |
(8.87b) |
dann heißt der Grenzwert (8.87b) der Hauptwert des uneigentlichen Integrals , auch CAUCHY scher Hauptwert .