Grundlage der FOURIER-Transformation ist das FOURIER-Integral, auch
Integralformel von FOURIER genannt:
Falls eine nichtperiodische Funktion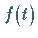 
in einem beliebigen endlichen Intervall den
DIRICHLETschen Bedingungen genügt und außerdem das Integral
 |
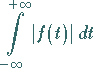(15.64a) |
konvergiert, dann gilt
 |
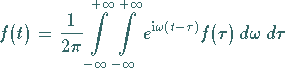(15.64b) |
in jedem Punkt, in dem die Funktion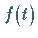
stetig ist, und
 |
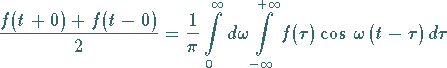(15.64c) |
in den Unstetigkeitsstellen.
