Unabhängigkeit vom Integrationsweg
Das Integral (14.33) einer Funktion einer komplexen Veränderlichen, die in
einem einfach zusammenhängenden Gebiet definiert ist und die zwei feste Punkte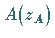 
und 
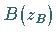miteinander verbindet, kann unabhängig vom Integrationsweg sein.
Notwendige und hinreichende Bedingung dafür ist, daß die Funktion in diesem Gebiet
analytisch ist, d.h., daß sie den
CAUCHY-RIEMANNschen Differentialgleichungen genügt.
Dann gilt (14.35).
Ein einfach zusammenhängendes Gebiet besitzt eine einzige geschlossene,
doppelpunktfreie Randkurve.
