Definition der analytischen Funktion
Eine Funktion 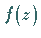 heißt in einem Gebiet
heißt in einem Gebiet 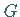 analytisch , regulär oder
holomorph , wenn sie in allen Punkten von
analytisch , regulär oder
holomorph , wenn sie in allen Punkten von 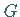 differenzierbar ist.
Randpunkte von
differenzierbar ist.
Randpunkte von 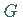 ,
in denen
,
in denen 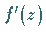 nicht existiert, sind singuläre Punkte von
nicht existiert, sind singuläre Punkte von
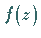 .
.
Die Funktion 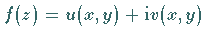 ist genau dann in
ist genau dann in 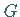 differenzierbar, wenn
differenzierbar, wenn
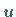 und
und 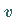 stetige partielle Ableitungen nach
stetige partielle Ableitungen nach 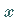 und
und 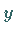 in
in 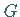 besitzen und dort die
CAUCHY-RIEMANNschen Differentialgleichungen gelten:
besitzen und dort die
CAUCHY-RIEMANNschen Differentialgleichungen gelten:
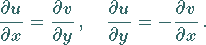 |
(14.4) |
Real- und Imaginärteil einer analytischen Funktion genügen für sich der
LAPLACEschen Differentialgleichung
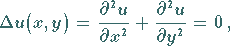 |
(14.5a) |
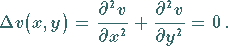 |
(14.5b) |
Die Ableitungen der elementaren Funktionen einer komplexen Veränderlichen werden nach
den gleichen Formeln berechnet wie die Ableitungen der entsprechenden Funktionen einer
reellen Veränderlichen.
| Beispiel A |
|
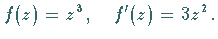
|
| Beispiel B |
|
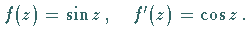
|