|
|
|
|
sei stetig in einem Gebiet 
,
in dem eine Kurve 
die Punkte 
und 
verbinden soll.
Die Kurve
wird zwischen den Punkten
und
durch beliebige Teilpunkte 
in
Teilbogen zerlegt (s. Abbildung).
heraus und bildet
 |
(14.32a) |
Existiert der Grenzwert
 |
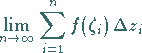(14.32b) |
mit 
für 
unabhängig von der Wahl
der Zwischenpunkte 
,
dann wird durch diesen Grenzwert das bestimmte
komplexe Integral
zwischen den Punkten
und 
,
dem Integrationsweg definiert.
Die Schreibweise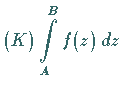 
bedeutet, daß das bestimmte komplexe
Integral längs der Kurve
zwischen den Punkten
und
zu berechnen ist.
Häufig wird für denselben Sachverhalt die Schreibweise
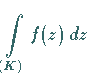bzw.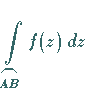 
verwendet.
|
|
