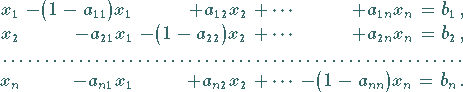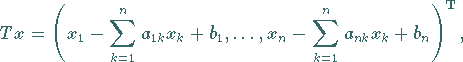Iterationsverfahren zur Lösung linearer Gleichungssysteme
Das gegebene lineare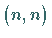 
-Gleichungssystem
 |
(12.60a) |
geht durch Umformung (s. Lineare Gleichungssysteme) gemäß
(19.26)in das äquivalente Gleichungssystem
 |
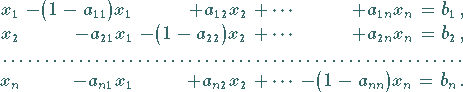(12.60b) |
über.
Dieses läßt sich mit dem Operator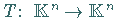 
,
definiert durch
 |
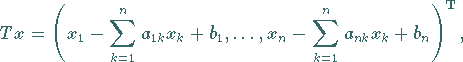(12.61) |
in das Fixpunktproblem
 |
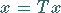(12.62) |
überführen, das im metrischen Raum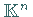 
,
versehen mit einer geeigneten Metrik,
der euklidischen (12.42), der Metrik (12.43) oder der Metrik
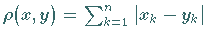(vgl. mit (12.45)), betrachtet wird.
Ist eine der Zahlen
 |
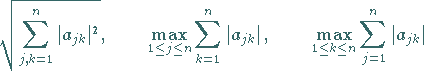(12.63) |
kleiner als 1, dann erweist sich 
als kontrahierender Operator und besitzt genau einen
Fixpunkt (s. BANACHscher Fixpunktsatz), der der
komponentenweise Grenzwert der Iterationsfolge mit beliebigem Startpunkt aus 
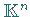ist.
