Banachscher Fixpunktsatz
Sei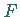 
eine nichtleere abgeschlossene Teilmenge eines vollständigen metrischen Raumes
.
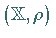Sei 
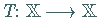ein kontraktiver Operator auf 
,
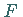d.h.,
es existiert eine Konstante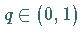 
,
so daß gilt
 |
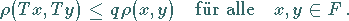(12.56) |
Dann gilt:
1. Für einen beliebigen Startpunkt 
ist das Iterationsverfahren
 |
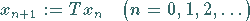(12.57) |
unbeschränkt ausführbar, d.h., für jedes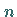 
gilt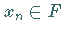 
.
2. Die Iterationsfolge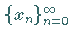 
konvergiert gegen ein Element
.
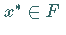3. Es gilt
 |
(12.58) |
4. Der einzige Fixpunkt von 
in
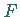ist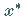 
.
5. Es gilt die Fehlerabschätzung
 |
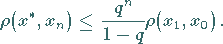(12.59) |
Im Zusammenhang mit dem BANACHschen Fixpunktsatz spricht man vom Prinzip der
kontrahierenden Abbildung oder dem Kontraktionsprinzip .
