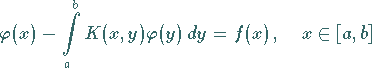Die FREDHOLMsche Integralgleichung 2. Art
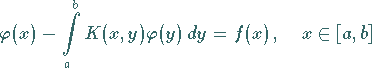 |
(12.64) |
mit stetigem Kern und stetiger rechter Seite kann man iterativ lösen, indem sie mit
Hilfe des Operators
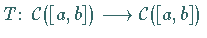 ,
definiert durch
,
definiert durch
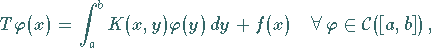 |
(12.65) |
in ein Fixpunktproblem 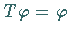 im metrischen Raum
im metrischen Raum 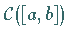 (s. Beispiel J) überführt und der Fixpunktsatz angewendet
wird, vorausgesetzt, es gilt
(s. Beispiel J) überführt und der Fixpunktsatz angewendet
wird, vorausgesetzt, es gilt 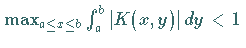 .
Die eindeutige Lösung erhält man als gleichmäßigen Grenzwert der Iterationsfolge
.
Die eindeutige Lösung erhält man als gleichmäßigen Grenzwert der Iterationsfolge
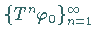 ,
beginnend mit einer beliebigen Funktion
,
beginnend mit einer beliebigen Funktion
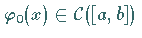 .
.